导数与微分 - 概率论前置知识

2.1 导数的定义与几何意义

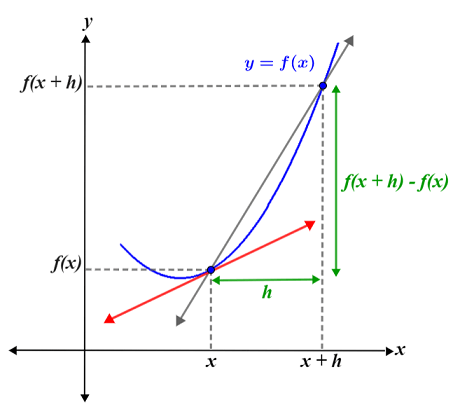
在微积分中，导数用于描述函数的变化率。对于概率论，导数在定义概率密度函数与分布函数的关系时十分重要。 如果函数 f(x) 在点 x = a 附近有定义，那么它在点 a 处的导数可以定义为：

$$f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}$$

几何意义上，导数表示曲线在某一点的切线斜率。这对于概率密度函数的斜率以及分布函数的变化速率是非常关键的理解。

图 1: 导数的几何意义——曲线在某一点的切线斜率

如上图所示，导数可以看作曲线在某一点处的瞬时变化率，这对于理解概率密度函数的变化具有直观的意义。

2.2 常见函数的导数与计算公式

在概率论中，我们经常会遇到多种常见函数，例如多项式函数、指数函数、对数函数和三角函数等。下面列出一些常见函数的导数计算公式：

• 常数函数： $$\frac{d}{dx}(c) = 0$$
• 幂函数： $$\frac{d}{dx}(x^n) = n x^{n-1}$$
• 指数函数： $$\frac{d}{dx}(e^x) = e^x$$ $$\frac{d}{dx}(a^x) = a^x \ln(a)$$
• 对数函数： $$\frac{d}{dx}(\ln(x)) = \frac{1}{x}, \quad x > 0$$ $$\frac{d}{dx}(\log_a(x)) = \frac{1}{x \ln(a)}, \quad x > 0$$
• 三角函数： $$\frac{d}{dx}(\sin(x)) = \cos(x)$$ $$\frac{d}{dx}(\cos(x)) = -\sin(x)$$ $$\frac{d}{dx}(\tan(x)) = \sec^2(x)$$
• 反三角函数： $$\frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1-x^2}}, \quad |x| < 1$$ $$\frac{d}{dx}(\arccos(x))=-\frac{1}{\sqrt{1-x^2}}, \quad |x| < 1$$ $$\frac{d}{dx}(\arctan(x))=\frac{1}{1+x^2}$$

掌握这些导数公式是进行概率论中的期望与方差计算的基础。

2.3 导数的运算法则

在概率论的学习过程中，经常需要对复合函数进行导数运算。因此，需要掌握一些基本的导数运算法则：

• 链式法则：如果 y = g(f(x))，那么其导数为： $$\frac{dy}{dx} = g'(f(x)) \cdot f'(x)$$
• 积的导数法则： $$\frac{d}{dx}[u(x) \cdot v(x)] = u'(x) v(x) + u(x) v'(x)$$
• 商的导数法则： $$\frac{d}{dx}\left(\frac{u(x)}{v(x)}\right) = \frac{u'(x)v(x) - u(x)v'(x)}{v(x)^2}$$

这些法则在处理概率密度函数或累积分布函数的推导中非常有用。

2.4 高阶导数(略)

高阶导数是对函数进行多次求导后的结果。对于函数 f(x)，其 n 阶导数表示为 f^(n)(x)。 高阶导数在概率论中用于描述更加复杂的变化趋势，例如加速度、凹凸性等。

第二阶导数（也称为二阶导数）常用来描述函数的凹凸性：

• 如果 f''(x) > 0，则函数在该点为凹形（向上开口）。
• 如果 f''(x) < 0，则函数在该点为凸形（向下开口）。

更高阶的导数（例如三阶、四阶等）用于描述函数更加复杂的变化行为。

2.5 对积分的求导

2.5.1 情况 1：积分的上限和下限是常数

假设我们有一个由积分表示的函数：

$$F(x) = \int_{a}^{b} f(t) \, dt$$

其中，$a$ 和 $b$ 都是常数。根据微积分基本定理，$F(x)$ 对 $x$ 的导数为零，因为积分的结果是一个常数，与 $x$ 无关。

2.5.2 情况 2：积分的上限是变量

如果积分的上限是变量 $x$，下限是常数 $a$，我们对函数

$$F(x) = \int_{a}^{x} f(t) \, dt$$

求导，根据微积分基本定理的第一部分，有：

$$\frac{d}{dx} F(x) = f(x)$$

这表明，对一个上限为 $x$ 的积分函数求导，等价于直接将上限代入被积函数。

2.5.3 情况 2 的变体：上限是 $g(x)$

如果积分的上限是一个函数 $g(x)$，而下限是常数 $a$，即：

$$F(x) = \int_{a}^{g(x)} f(t) \, dt$$

那么对 $F(x)$ 求导时，我们使用莱布尼兹积分规则，公式为：

$$\frac{d}{dx} F(x) = f(g(x)) \cdot g'(x)$$

步骤如下：

• 首先，将上限 $g(x)$ 代入被积函数 $f(t)$，得到 $f(g(x))$。
• 然后，应用链式法则，对 $g(x)$ 求导，得到 $g'(x)$。

2.5.4 情况 3：上限和下限都是变量

如果积分的上限和下限都是变量，例如：

$$F(x) = \int_{u(x)}^{v(x)} f(t) \, dt$$

则我们使用莱布尼兹积分规则，公式为：

$$\frac{d}{dx} \left( \int_{u(x)}^{v(x)} f(t) \, dt \right) = f(v(x)) \cdot v'(x) - f(u(x)) \cdot u'(x)$$

这意味着我们要分别对上限和下限应用链式法则，并将结果相减。

2.5.5 情况 4：被积函数包含变量

如果被积函数本身包含变量 $x$，例如：

$$F(x) = \int_{a}^{b} f(t, x) \, dt$$

则我们在求导时使用链式法则，得到：

$$\frac{d}{dx} F(x) = \int_{a}^{b} \frac{\partial}{\partial x} f(t, x) \, dt$$

这表明我们需要对被积函数相对于 $x$ 求偏导，然后再对整个表达式积分。