积分 - 概率论前置知识
3.1 不定积分的定义与基本性质
不定积分是求原函数的过程，即找到一个函数 F(x)，使得其导数等于给定函数 f(x)。
数学上表示为：
$$
F'(x) = f(x) \implies \int f(x) \, dx = F(x) + C
$$
例：\( (x^2)' = 2x \)，所以 \( \int 2x \, dx = x^2 + C \)。\( x^2 + 1 \)、\( x^2 - 5 \) 的导数也都是 \( 2x \)，这就是要加 \( C \) 的原因。
其中，C 是积分常数，表示任意一个常数，因为导数对常数求导结果为零。
3.2 定积分与面积
定积分用于求某一函数在特定区间上的累积量，通常表示为区间 [a, b] 上函数 f(x) 的定积分：
$$
\int_a^b f(x) \, dx
$$
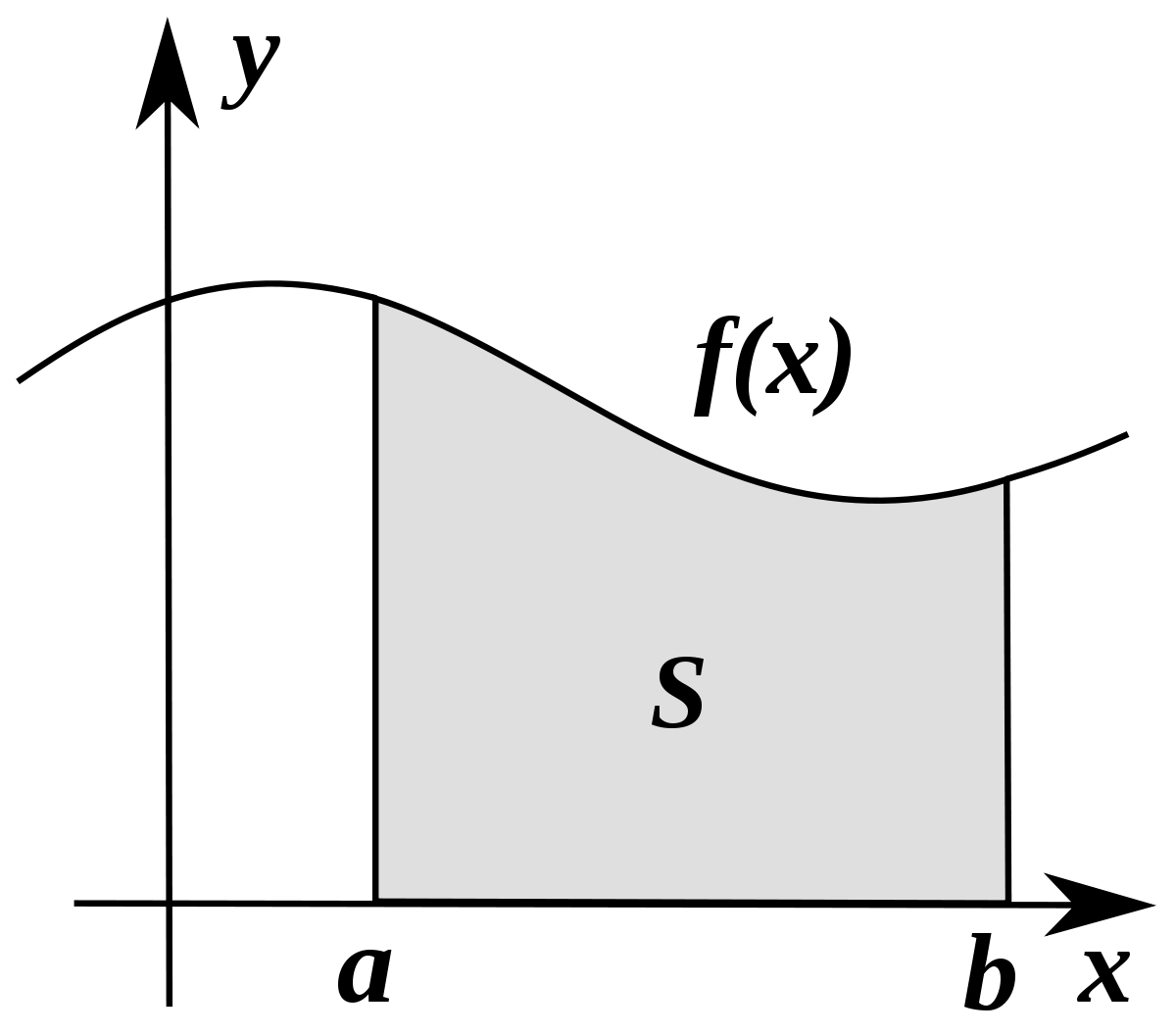
定积分的几何意义是曲线 f(x) 与 x 轴之间在区间 [a, b] 上所围成的区域的面积。当 f(x) 在该区间内为正时，定积分表示面积；若 f(x) 为负，则表示有符号面积。
例：\( \int_0^2 x \, dx = 2 \)，正好是底为 2、高为 2 的三角形面积；\( \int_{-1}^0 x \, dx = -\frac{1}{2} \)，曲线在 x 轴下方，结果为负。
在概率论中，定积分被用于计算连续随机变量的概率。例如，概率密度函数在某区间上的积分表示该区间内随机变量取值的概率。
3.3 积分的基本性质与计算法则
积分运算具有以下几个基本性质和计算法则，这些性质对于求解积分非常重要：
- 线性性质：
$$
\int (a f(x) + b g(x)) \, dx = a \int f(x) \, dx + b \int g(x) \, dx
$$
其中 a, b 为常数。
例：\( \int (3x^2 + 4x) \, dx = 3 \cdot \frac{x^3}{3} + 4 \cdot \frac{x^2}{2} = x^3 + 2x^2 + C \)
- 区间可加性：
$$
\int_a^b f(x) \, dx + \int_b^c f(x) \, dx = \int_a^c f(x) \, dx
$$
例：\( \int_0^1 x \, dx + \int_1^2 x \, dx = \frac{1}{2} + \frac{3}{2} = 2 = \int_0^2 x \, dx \)
- 牛顿-莱布尼茨公式：
$$
\int_a^b f(x) \, dx = F(b) - F(a)
$$
其中 F(x) 是 f(x) 的一个原函数。
例：\( 2x \) 的原函数是 \( x^2 \)，所以 \( \int_1^3 2x \, dx = 3^2 - 1^2 = 8 \)
这些性质和计算法则在概率论中被用于计算累积分布函数、期望值以及方差等关键量。
3.4 常见函数的积分公式
下面列出一些常见函数的积分公式，供复习参考：
- 幂函数：
$$
\int x^n \, dx = \frac{x^{n+1}}{n+1} + C, \quad n \neq -1
$$
例：\( \int x^2 \, dx = \frac{x^3}{3} + C \)；\( \int_0^1 x^2 \, dx = \frac{1}{3} \)
- 指数函数：
$$
\int e^x \, dx = e^x + C
$$
例：\( \int_0^1 e^x \, dx = e^1 - e^0 = e - 1 \)
$$
\int a^x \, dx = \frac{a^x}{\ln(a)} + C, \quad a > 0, a \neq 1
$$
例：\( \int 2^x \, dx = \frac{2^x}{\ln 2} + C \)
- 对数函数：
$$
\int \frac{1}{x} \, dx = \ln|x| + C
$$
例：\( \int_1^e \frac{1}{x} \, dx = \ln e - \ln 1 = 1 \)
- 三角函数：
$$
\int \sin(x) \, dx = -\cos(x) + C
$$
例：\( \int_0^\pi \sin x \, dx = -\cos\pi + \cos 0 = 2 \)
$$
\int \cos(x) \, dx = \sin(x) + C
$$
例：\( \int_0^{\pi/2} \cos x \, dx = \sin\frac{\pi}{2} - \sin 0 = 1 \)
$$
\int \sec^2(x) \, dx = \tan(x) + C
$$
例：\( \int_0^{\pi/4} \sec^2 x \, dx = \tan\frac{\pi}{4} - \tan 0 = 1 \)
3.5 带参数的积分（累积分布函数）
带参数的积分是指上限或下限为变量的积分，这在概率论中十分常见，例如累积分布函数的定义。一般形式如下：
$$
F(x) = \int_{-\infty}^x f(t) \, dt
$$
这里，F(x) 表示函数 f(t) 在区间 \((-\infty, x]\) 上的累积量。当 f(t) 为概率密度函数时，F(x) 即为累积分布函数，表示随机变量小于等于 x 的概率。
例：指数分布的密度为 \( f(t) = e^{-t} \)（\( t \ge 0 \)，\( t < 0 \) 时为 0）。当 \( x \ge 0 \) 时，\( F(x) = \int_0^x e^{-t} \, dt = 1 - e^{-x} \)，例如 \( F(1) = 1 - e^{-1} \approx 0.632 \)。
利用基本微积分知识，可以得出累积分布函数 F(x) 与概率密度函数 f(x) 的关系为：
$$
F'(x) = f(x)
$$
例：接上例，\( (1 - e^{-x})' = e^{-x} = f(x) \)。
这种带参数的积分在概率论中用于描述随机变量在不同区间上的累积概率，是理解概率密度与分布函数之间关系的关键。
见：正态分布的示例
