# 以下都是例行公事,直接拷贝即可
import pandas as pd
import numpy as np
# 导入matplotlib.pyplot绘图库,其中plt.plot()是最常用的绘图函数之一
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme() # 默认用seaborn的绘图样式
# 设置字体。如果不设置,中文可能会乱码。这里采用冬青黑、微软雅黑和文泉驿微米黑,可以兼容大多数操作系统。
plt.rcParams["font.sans-serif"]=[ "Microsoft YaHei", "Hiragino Sans GB", "WenQuanYi Micro Hei"]
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题
# 绘图使用'svg'后端:svg是矢量格式,可以任意缩放均保持清晰,各种屏幕的显示良好。
%config InlineBackend.figure_formats = ['svg']29 基础案例
本章主要讲解参考书《Python金融数据分析与挖掘实战》中的第7章:基础案例。按照我们前面所学的知识以及作业,这几个案例应该都可以顺利完成。
注:
- 不需要你手中有这本书。本讲义已经包括了对案例的描述,数据会发送给大家。
- 虽然题目来自参考书,但原书中的“写法”可能有一些问题,因此这里以我们自己的写法为主。如果有书,大家可以对比看看。
- 数据统一放在工作目录的
data/case??/目录下,如原书案例7.2,数据在data/case7.2/下
数据下载地址 https://py4ss.net/python/data.zip
29.1 股票价格指数周收益率和月收益率的计算
(原7.2节, p139)
29.1.1 要求
从excel文件中读取股票的日线价格,然后计算“周收益率”和“月收益率”。
IDX_Idxtrd.xlsx包括股票价格TRD_Cale.xlsx包括每个日期是星期几(在我们的做法中用不到)
29.1.2 思路和实现
- 读取数据,修正每一列的数据类型。
- 用
set_index()转为时间序列。 - 用
resample()把日线转为周线和月线,均选择收盘价。 - 用
pct_change()分别计算周和月的收益率。
当然,如果有需要,你也可以用差分来计算。
注意:
教材的算法不对。收益率是“本周期的期末价格”相对“上一个周期的期末价格”的变化率。 如果是日频,则是今天收盘价相对上一个交易日的收盘价的变化。如果是周频,则是本周最后一天的收盘价,相对上一周最后一天收盘价的变化。而不是最后一天的价格相对第一天的价格的变化。
教材的做法不佳。应优先使用Python、NumPy和Pandas提供函数,不能满足需求再自己写算法。即使自己写算法,优先考虑序列化操作(ndarray的广播,或者Series都可以支持),最后才考虑用循环。
# 读取数据并查看
df = pd.read_excel('data/case7.2/IDX_Idxtrd.xlsx')
df.head() | Indexcd | Idxtrd01 | Idxtrd05 | |
|---|---|---|---|
| 0 | 2 | 2017-01-03 | 3283.45 |
| 1 | 2 | 2017-01-04 | 3307.45 |
| 2 | 2 | 2017-01-05 | 3314.39 |
| 3 | 2 | 2017-01-06 | 3302.79 |
| 4 | 2 | 2017-01-09 | 3320.53 |
df.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 244 entries, 0 to 243
Data columns (total 3 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Indexcd 244 non-null int64
1 Idxtrd01 244 non-null object
2 Idxtrd05 244 non-null float64
dtypes: float64(1), int64(1), object(1)
memory usage: 5.8+ KB观察结果:
- 只有1只股票,因此股票代码列用不到,因此虽然这里类型错了,但可以不用处理(回忆对应章节)。
- 日期列是str,要修正,价格列没问题。
- 每列的名字要改,中英文皆可,但是要顾名思义,不能用无意义的代号。
price_d = df.iloc[:,[1,2]]
price_d.columns = ['date','close']
price_d.head()| date | close | |
|---|---|---|
| 0 | 2017-01-03 | 3283.45 |
| 1 | 2017-01-04 | 3307.45 |
| 2 | 2017-01-05 | 3314.39 |
| 3 | 2017-01-06 | 3302.79 |
| 4 | 2017-01-09 | 3320.53 |
处理成时间序列数据
# 要利用Pandas时间序列的特性,首先要把数据转为时间序列格式
price_d['date'] = pd.to_datetime(price_d['date'])
price_d.set_index('date',inplace=True)
price_d.head()
# 从原始数据中整理得到的时间序列数据就完成了。
# 检验过数据没问题,这个警告可以无视。/tmp/ipykernel_3691/753111952.py:2: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
price_d['date'] = pd.to_datetime(price_d['date'])| close | |
|---|---|
| date | |
| 2017-01-03 | 3283.45 |
| 2017-01-04 | 3307.45 |
| 2017-01-05 | 3314.39 |
| 2017-01-06 | 3302.79 |
| 2017-01-09 | 3320.53 |
简单绘制一下价格走势图
price_d.plot();日线转周线:注意resample只能用在时间序列数据上。
price_w = price_d.resample('W').last()
price_w.head()| close | |
|---|---|
| date | |
| 2017-01-08 | 3302.79 |
| 2017-01-15 | 3259.27 |
| 2017-01-22 | 3270.33 |
| 2017-01-29 | 3308.06 |
| 2017-02-05 | 3288.17 |
计算周回报率:在周线上调用方法pct_change()。
# 计算周回报率
price_w['return'] = price_w['close'].pct_change(fill_method=None).round(4)
price_w.head()| close | return | |
|---|---|---|
| date | ||
| 2017-01-08 | 3302.79 | NaN |
| 2017-01-15 | 3259.27 | -0.0132 |
| 2017-01-22 | 3270.33 | 0.0034 |
| 2017-01-29 | 3308.06 | 0.0115 |
| 2017-02-05 | 3288.17 | -0.0060 |
同样的方法计算月线和月回报率。
# 转为月线:每月最后一天的收盘价
price_m = price_d.resample('ME').last()
price_m.head()| close | |
|---|---|
| date | |
| 2017-01-31 | 3308.06 |
| 2017-02-28 | 3394.50 |
| 2017-03-31 | 3374.67 |
| 2017-04-30 | 3303.44 |
| 2017-05-31 | 3264.54 |
# 计算月回报率
price_m['return'] = price_m['close'].pct_change().round(4)
price_m.head()| close | return | |
|---|---|---|
| date | ||
| 2017-01-31 | 3308.06 | NaN |
| 2017-02-28 | 3394.50 | 0.0261 |
| 2017-03-31 | 3374.67 | -0.0058 |
| 2017-04-30 | 3303.44 | -0.0211 |
| 2017-05-31 | 3264.54 | -0.0118 |
# 简单验算
3394.50 / 3308.06 - 10.02613011855891378429.2 上市公司净利润增长率
(原7.3小节,p143)
29.2.1 要求
从数据中找出连续3年,净利润增长率都在40%以上的公司。
data2.xlsx:利润表info.xlsx:股票代码、简称和行业
29.2.2 思路和实现
merge()按代码列合并数据groupby()按代码分组,pct_change()计算百分比变化(分组后显然就是每个股票自己和自己相比,利润的年度增长率)groupby()按代码分组,循环每个组。
# 例行公事,一般一个ipynb或者.py文件最前面import一次即可
import pandas as pd
import numpy as np
df1 = pd.read_excel('data/case7.3/data2.xlsx',converters={'Stkcd':str, 'Accper':pd.to_datetime})
df1.head()| Stkcd | Accper | B002000101 | |
|---|---|---|---|
| 0 | 000016 | 2014-12-31 | 5.262353e+07 |
| 1 | 000016 | 2015-12-31 | -1.256819e+09 |
| 2 | 000016 | 2016-12-31 | 9.567303e+07 |
| 3 | 000016 | 2017-12-31 | 5.057025e+09 |
| 4 | 000020 | 2014-12-31 | 7.687620e+06 |
df2 = pd.read_excel('data/info.xlsx',converters = {'Stkcd':str})
df2.head()| Stkcd | Stknme | Nnindnme | |
|---|---|---|---|
| 0 | 000016 | 深康佳A | 计算机、通信和其他电子设备制造业 |
| 1 | 000020 | 深华发A | 计算机、通信和其他电子设备制造业 |
| 2 | 000021 | 深科技 | 计算机、通信和其他电子设备制造业 |
| 3 | 000045 | 深纺织A | 计算机、通信和其他电子设备制造业 |
| 4 | 000050 | 深天马A | 计算机、通信和其他电子设备制造业 |
# 检查一下数据,行业名称去重,查看有几个行业:
# 回忆作业1:我们做过自己的unique函数。
df2.Nnindnme.unique()array(['计算机、通信和其他电子设备制造业'], dtype=object)把2个数据按股票代码列进行合并,我们可以对这个新数据进行处理。
# merge两个数据,去掉行业列,因为行业全部相同。
profit_y = df1.merge(df2).drop('Nnindnme',axis=1)
profit_y.columns = ['股票代码','会计年度','净利润','股票简称']
profit_y.head()| 股票代码 | 会计年度 | 净利润 | 股票简称 | |
|---|---|---|---|---|
| 0 | 000016 | 2014-12-31 | 5.262353e+07 | 深康佳A |
| 1 | 000016 | 2015-12-31 | -1.256819e+09 | 深康佳A |
| 2 | 000016 | 2016-12-31 | 9.567303e+07 | 深康佳A |
| 3 | 000016 | 2017-12-31 | 5.057025e+09 | 深康佳A |
| 4 | 000020 | 2014-12-31 | 7.687620e+06 | 深华发A |
求每只股票的年度净利润增长率:先按股票分组,再对净利润列调用pct_change()求百分比变化。
growth = profit_y.groupby('股票代码')['净利润'].pct_change()
profit_y['增长率'] = growth
profit_y.head(8)| 股票代码 | 会计年度 | 净利润 | 股票简称 | 增长率 | |
|---|---|---|---|---|---|
| 0 | 000016 | 2014-12-31 | 5.262353e+07 | 深康佳A | NaN |
| 1 | 000016 | 2015-12-31 | -1.256819e+09 | 深康佳A | -24.883220 |
| 2 | 000016 | 2016-12-31 | 9.567303e+07 | 深康佳A | -1.076123 |
| 3 | 000016 | 2017-12-31 | 5.057025e+09 | 深康佳A | 51.857375 |
| 4 | 000020 | 2014-12-31 | 7.687620e+06 | 深华发A | NaN |
| 5 | 000020 | 2015-12-31 | -4.200846e+06 | 深华发A | -1.546443 |
| 6 | 000020 | 2016-12-31 | 5.457710e+06 | 深华发A | -2.299193 |
| 7 | 000020 | 2017-12-31 | 9.744094e+05 | 深华发A | -0.821462 |
注意:假如不按股票分组,直接取净利润求增长率,那么就会出现某一只股票的第一个利润,减去前一只股票最后一个利润的情况。
如上表:
- 第4行,深华发2014年的增速,因为我们没有2013年的数据,因此无法计算,结果显示NA是正确的。
- 如果不分组,则会使用深华发2014年的利润(第4行)和深康佳2017年(第3行)进行比较,显然并不正确。
对分组进行循环,我们就可以更明显第看到这一点。
# 先罗列一下前几只股票
for i,x in profit_y.iloc[:12].groupby('股票代码'):
display(x) # 类似于print()函数,display()也可以把数据显示出来,但对于DataFrame的显示比较好| 股票代码 | 会计年度 | 净利润 | 股票简称 | 增长率 | |
|---|---|---|---|---|---|
| 0 | 000016 | 2014-12-31 | 5.262353e+07 | 深康佳A | NaN |
| 1 | 000016 | 2015-12-31 | -1.256819e+09 | 深康佳A | -24.883220 |
| 2 | 000016 | 2016-12-31 | 9.567303e+07 | 深康佳A | -1.076123 |
| 3 | 000016 | 2017-12-31 | 5.057025e+09 | 深康佳A | 51.857375 |
| 股票代码 | 会计年度 | 净利润 | 股票简称 | 增长率 | |
|---|---|---|---|---|---|
| 4 | 000020 | 2014-12-31 | 7687620.27 | 深华发A | NaN |
| 5 | 000020 | 2015-12-31 | -4200845.61 | 深华发A | -1.546443 |
| 6 | 000020 | 2016-12-31 | 5457710.33 | 深华发A | -2.299193 |
| 7 | 000020 | 2017-12-31 | 974409.39 | 深华发A | -0.821462 |
| 股票代码 | 会计年度 | 净利润 | 股票简称 | 增长率 | |
|---|---|---|---|---|---|
| 8 | 000021 | 2014-12-31 | 1.756764e+08 | 深科技 | NaN |
| 9 | 000021 | 2015-12-31 | 1.806603e+08 | 深科技 | 0.028370 |
| 10 | 000021 | 2016-12-31 | 2.144235e+08 | 深科技 | 0.186888 |
| 11 | 000021 | 2017-12-31 | 5.413030e+08 | 深科技 | 1.524457 |
继续对分组数据进行循环,提取”增长率最后3个值全部大于等于0.4”的组。
# 开始循环每只股票的分组DataFrame
# 如果符合要求(三年净利润增速都>=0.4),添加到空列表result
result = []
for i,x in profit_y.groupby('股票代码'):
if all(x['增长率'].tail(3) >= 0.4):
result.append(x)
result = pd.concat(result)
result.head(8)| 股票代码 | 会计年度 | 净利润 | 股票简称 | 增长率 | |
|---|---|---|---|---|---|
| 286 | 002383 | 2014-12-31 | 4.005807e+07 | 合众思壮 | NaN |
| 287 | 002383 | 2015-12-31 | 6.057712e+07 | 合众思壮 | 0.512233 |
| 288 | 002383 | 2016-12-31 | 9.644973e+07 | 合众思壮 | 0.592181 |
| 289 | 002383 | 2017-12-31 | 2.419267e+08 | 合众思壮 | 1.508319 |
| 310 | 002402 | 2014-12-31 | 4.505389e+07 | 和而泰 | NaN |
| 311 | 002402 | 2015-12-31 | 7.494657e+07 | 和而泰 | 0.663487 |
| 312 | 002402 | 2016-12-31 | 1.196604e+08 | 和而泰 | 0.596609 |
| 313 | 002402 | 2017-12-31 | 1.781037e+08 | 和而泰 | 0.488410 |
29.2.3 长表和宽表的转换
首先构造一个示例数据:这是一个最一般的时间序列数据:ABC个观察对象(人或者公司等等),在2022-01-01到2022-01-03这三天里的某个属性。
比如:3家上市公司3天的股价;3个人3天的心情指数;等等。
# 构造示例数据
df_long = pd.DataFrame({'date': list(pd.date_range('2022-01-01', '2022-01-03'))*3,
'name': ['A']*3 + ['B']*3 + ['C']*3,
'value': np.random.randint(1, 10, 9)})
df_long| date | name | value | |
|---|---|---|---|
| 0 | 2022-01-01 | A | 1 |
| 1 | 2022-01-02 | A | 8 |
| 2 | 2022-01-03 | A | 5 |
| 3 | 2022-01-01 | B | 1 |
| 4 | 2022-01-02 | B | 4 |
| 5 | 2022-01-03 | B | 9 |
| 6 | 2022-01-01 | C | 1 |
| 7 | 2022-01-02 | C | 1 |
| 8 | 2022-01-03 | C | 2 |
这是一个“长数据 long data”:
- 每一列是一个属性。
- 每一行有1个或者多个观测值。比如第一行是被观察对象A在2022年1月1日的某个属性,值为3。
因为每一列都是一个属性,因此你可以通过简单的行筛选列来找到你要的值。
df_long[(df_long['date'] == "2022-01-02") & (df_long['name'] == 'B')]| date | name | value | |
|---|---|---|---|
| 4 | 2022-01-02 | B | 4 |
宽数据则不同:行标签表示某个(或者几个)属性的取值,列标签表示另一个(或者几个)属性的取值,表格的内容就是数据。
下表是个“宽数据”:
- 行标签是日期,列标签是姓名
- 行和列(日期-姓名)共同指示一个数据。
df_wide = df_long.pivot(index = 'date',columns = 'name',values = 'value')
df_wide| name | A | B | C |
|---|---|---|---|
| date | |||
| 2022-01-01 | 1 | 1 | 1 |
| 2022-01-02 | 8 | 4 | 1 |
| 2022-01-03 | 5 | 9 | 2 |
因此选择数据往往要同时选择行和列:
df_wide.loc['2022-01-02','B']4长数据转宽数据,使用 .pivot(),3个参数:
- index: 选择那一列(或者几列),作为宽表的行标签(你希望行是什么?这里选择每行是一个人)
- columns: 选择那一列(或者几列),作为宽表的列标签(你希望列是什么?这里选择每列是日期)
- value: 行列所决定的数据。
df_long.pivot(index = 'name',columns = 'date',values = 'value')| date | 2022-01-01 | 2022-01-02 | 2022-01-03 |
|---|---|---|---|
| name | |||
| A | 1 | 8 | 5 |
| B | 1 | 4 | 9 |
| C | 1 | 1 | 2 |
注意,这个宽表和前面的宽表不同:行列正好对换。同样的长表,可能因为你选择不同的行或者列,可以形成不同的宽表,但含义是一样的。选择什么作为行和列,主要看对表格的要求,或者对后续分析的便利。
那么宽表转长表呢?用.stack(),恰好是长转宽反过来。
df_wide.stack().reset_index() # 注意列名是0,你要手动改一下,这里略| date | name | 0 | |
|---|---|---|---|
| 0 | 2022-01-01 | A | 1 |
| 1 | 2022-01-01 | B | 1 |
| 2 | 2022-01-01 | C | 1 |
| 3 | 2022-01-02 | A | 8 |
| 4 | 2022-01-02 | B | 4 |
| 5 | 2022-01-02 | C | 1 |
| 6 | 2022-01-03 | A | 5 |
| 7 | 2022-01-03 | B | 9 |
| 8 | 2022-01-03 | C | 2 |
29.2.4 回到案例
查看我们的数据:
result.head(8)| 股票代码 | 会计年度 | 净利润 | 股票简称 | 增长率 | |
|---|---|---|---|---|---|
| 286 | 002383 | 2014-12-31 | 4.005807e+07 | 合众思壮 | NaN |
| 287 | 002383 | 2015-12-31 | 6.057712e+07 | 合众思壮 | 0.512233 |
| 288 | 002383 | 2016-12-31 | 9.644973e+07 | 合众思壮 | 0.592181 |
| 289 | 002383 | 2017-12-31 | 2.419267e+08 | 合众思壮 | 1.508319 |
| 310 | 002402 | 2014-12-31 | 4.505389e+07 | 和而泰 | NaN |
| 311 | 002402 | 2015-12-31 | 7.494657e+07 | 和而泰 | 0.663487 |
| 312 | 002402 | 2016-12-31 | 1.196604e+08 | 和而泰 | 0.596609 |
| 313 | 002402 | 2017-12-31 | 1.781037e+08 | 和而泰 | 0.488410 |
我们可以转为:每行是“股票代码+名称”,每列是“会计年度”,数据是“增长率”
result.pivot(index=['股票代码', '股票简称'], columns=['会计年度'],
values=['增长率']).dropna(axis=1).round(2)| 增长率 | ||||
|---|---|---|---|---|
| 会计年度 | 2015-12-31 | 2016-12-31 | 2017-12-31 | |
| 股票代码 | 股票简称 | |||
| 002383 | 合众思壮 | 0.51 | 0.59 | 1.51 |
| 002402 | 和而泰 | 0.66 | 0.60 | 0.49 |
| 002600 | 领益智造 | 11.95 | 4.08 | 5.00 |
| 300053 | 欧比特 | 1.31 | 0.46 | 0.43 |
| 300088 | 长信科技 | 0.43 | 0.46 | 0.57 |
| 300136 | 信维通信 | 2.51 | 1.40 | 0.67 |
| 300232 | 洲明科技 | 0.87 | 0.47 | 0.71 |
| 300296 | 利亚德 | 1.05 | 1.02 | 0.81 |
| 600260 | 凯乐科技 | 1.52 | 0.52 | 3.06 |
| 600330 | 天通股份 | 4.39 | 0.51 | 0.42 |
| 600667 | 太极实业 | 0.66 | 8.86 | 0.80 |
或者:每行“会计年度”,每列是“股票代码+名称”,数据是“增长率”
result.pivot(index=['会计年度'], columns=['股票代码', '股票简称'],
values=['增长率']).dropna(axis=0).round(2)| 增长率 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 股票代码 | 002383 | 002402 | 002600 | 300053 | 300088 | 300136 | 300232 | 300296 | 600260 | 600330 | 600667 |
| 股票简称 | 合众思壮 | 和而泰 | 领益智造 | 欧比特 | 长信科技 | 信维通信 | 洲明科技 | 利亚德 | 凯乐科技 | 天通股份 | 太极实业 |
| 会计年度 | |||||||||||
| 2015-12-31 | 0.51 | 0.66 | 11.95 | 1.31 | 0.43 | 2.51 | 0.87 | 1.05 | 1.52 | 4.39 | 0.66 |
| 2016-12-31 | 0.59 | 0.60 | 4.08 | 0.46 | 0.46 | 1.40 | 0.47 | 1.02 | 0.52 | 0.51 | 8.86 |
| 2017-12-31 | 1.51 | 0.49 | 5.00 | 0.43 | 0.57 | 0.67 | 0.71 | 0.81 | 3.06 | 0.42 | 0.80 |
29.3 股票价、量走势图的绘制
(原7.4小节 p145)
29.3.1 要求
绘制股价的走势曲线、日成交量柱状图、月成交量的饼图,以及三图并列。
数据:
trd.xlsx:3只股票的股价序列:长数据(回忆上一节)
df = pd.read_excel(
'data/case7.4/trd.xlsx', converters={'股票代码': str, '交易日期': pd.to_datetime})
df.head()| 股票代码 | 交易日期 | 收盘价 | 交易量 | |
|---|---|---|---|---|
| 0 | 600000 | 2017-01-03 | 16.30 | 16237125 |
| 1 | 600000 | 2017-01-04 | 16.33 | 29658734 |
| 2 | 600000 | 2017-01-05 | 16.30 | 26437646 |
| 3 | 600000 | 2017-01-06 | 16.18 | 17195598 |
| 4 | 600000 | 2017-01-09 | 16.20 | 14908745 |
# 看一下都有什么股票
df['股票代码'].unique()array(['600000', '600004', '600005'], dtype=object)29.3.2 价格曲线
问题1: 绘制600000股票,2017-01-03
:’2017-01-20’之间的收盘价
- 选股,选列,形成时间序列数据
- 筛选时间段
- 绘图
code = '600000'
x = df.query('股票代码 == @code ')[['交易日期', '收盘价']
].set_index('交易日期').loc['2017-01-03':'2017-01-20']
p1 = x.plot(legend=None) # 绘图时去掉 legend
# plt.xlim(('2016-12-31','2017-01-22'))
plt.ylabel('收盘价')
plt.title(f'{code}价格走势图')Text(0.5, 1.0, '600000价格走势图')29.3.3 日交易量
问题2:绘制60000,1月份的交易量柱状图
- 选股,选列,构造时间序列数据
- 选择时间段
- 绘图
(和上一题没什么区别)
y = df.query('股票代码 == @code ')[['交易日期','交易量']].set_index('交易日期').loc['2017-01']
p2 = y['交易量'].plot.bar();注意到,因为我们的index用的是datetime格式(pd.to_datetime),含有日期和时间信息,但我们只想显示日期,或者“月-日”,可以考虑日期格式化。
- 对于
DatetimeIndex数据(索引中的日期),调用.strftime()。 - 对于
Series数据(普通列中的日期),则是.dt.strftime()
参数是格式化字符串,常用的符号包括:
- %y 两位数的年份表示(00-99)
- %Y 四位数的年份表示(000-9999)
- %m 月份(01-12)
- %d 月内中的一天(0-31)
- %H 24小时制小时数(0-23)
- %I 12小时制小时数(01-12)
- %M 分钟数(00=59)
- %S 秒(00-59)
如”%Y-%m-%d”就是四位数的年-月-日。
# y是一个时间序列数据,index是datetime格式,包含日期和时间数据(顾名思义)
y.indexDatetimeIndex(['2017-01-03', '2017-01-04', '2017-01-05', '2017-01-06',
'2017-01-09', '2017-01-10', '2017-01-11', '2017-01-12',
'2017-01-13', '2017-01-16', '2017-01-17', '2017-01-18',
'2017-01-19', '2017-01-20', '2017-01-23', '2017-01-24',
'2017-01-25', '2017-01-26'],
dtype='datetime64[ns]', name='交易日期', freq=None)# 格式化为'月-日',看看效果
y.index.strftime("%m-%d")Index(['01-03', '01-04', '01-05', '01-06', '01-09', '01-10', '01-11', '01-12',
'01-13', '01-16', '01-17', '01-18', '01-19', '01-20', '01-23', '01-24',
'01-25', '01-26'],
dtype='object', name='交易日期')使用p.set_xticklabels(),把x坐标的标签(x坐标刻度上的文字),设置为你指定的列表。
y = df.query('股票代码 == @code ')[['交易日期','交易量']].set_index('交易日期').loc['2017-01']
y['交易量_亿'] = round(y['交易量']/10000000,2)
p2 = y['交易量_亿'].plot.bar();
p2.set_xticklabels(y.index.strftime("%m-%d")); # 改一下横坐标刻度上的标签
# 其他部分
plt.xticks(rotation=60);
plt.ylabel('成交量(亿)')
plt.xlabel('')Text(0.5, 0, '')29.3.4 月成交量饼图
问题3:绘制股票60000,从1月到11月的成交量的饼图
- 选择列:交易日期和交易量,设置为时间序列数据
.resample('ME').sum()重采样为月并求和:得到月交易量的和。- 生成一列“月”:1-11月
- 绘图!
code = '600000'
x = df.query('股票代码 == @code ')[['交易日期','交易量']].set_index('交易日期').resample("ME").sum().reset_index()
x| 交易日期 | 交易量 | |
|---|---|---|
| 0 | 2017-01-31 | 302255420 |
| 1 | 2017-02-28 | 278793913 |
| 2 | 2017-03-31 | 446555984 |
| 3 | 2017-04-30 | 426042150 |
| 4 | 2017-05-31 | 1086178385 |
| 5 | 2017-06-30 | 1330750427 |
| 6 | 2017-07-31 | 1317190884 |
| 7 | 2017-08-31 | 1369766042 |
| 8 | 2017-09-30 | 742796792 |
| 9 | 2017-10-31 | 522531066 |
| 10 | 2017-11-30 | 455222518 |
# 用时间方法`.dt.month()`,从交易日期列(Series)中提取月
trade_month = pd.Series(x['交易日期'].dt.month,name='月')
trade_month0 1
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
10 11
Name: 月, dtype: int32几个参数:
textprops:改标签的字体属性,这里改字号为10号。pctdistance:百分比标签的位置:从圆心为0,到圆周为1。
# 绘图!标签字体10号,百分比放在0.8的位置上
p3 = x.set_index(trade_month)['交易量'].plot.pie(
autopct='%.2f%%', textprops={'fontsize': 10}, pctdistance=0.8);
plt.ylabel('')
plt.title('月成交量分布');三图并列比较简单,这里略过。可以参考绘图章节的内容,下一个案例中也有更复杂的例子。
29.4 股票价格移动平均线的绘制
(原7.5小节 p149)
29.4.1 要求
对数据中所有的股票,绘制股票的价格和10日均线。绘图4个一组,并按2x2的格式排列,绘制全部股票。
数据:
trd.xlsx:股票代码、交易日、收盘价的数据(长表),注意和前面有个数据重名,这份数据在data/case7.5目录下。
29.4.2 原理和实现
依然贯彻我们的思路:
先按目标,把数据制作成符合要求的1个DataFrame,再对这个成品DF进行其他处理,如统计、绘制等。避免把数据整理、列运算、分析和绘制写在一段代码中!
- 测试如何绘制1只股票的价格和均线。
- 绘制4只股票在一张图中,写成一个函数。
- 把股票代码4个一组,分成n段,形成一个列表。
- 循环上述列表,调用第2步的函数。
29.4.3 读取数据
df = pd.read_excel('data/case7.5/trd.xlsx',
converters={'Stkcd':str,'Trddt':pd.to_datetime})
df.head()| Stkcd | Trddt | Clsprc | |
|---|---|---|---|
| 0 | 002001 | 2016-05-03 | 20.99 |
| 1 | 002001 | 2016-05-04 | 20.42 |
| 2 | 002001 | 2016-05-05 | 20.49 |
| 3 | 002001 | 2016-05-06 | 18.70 |
| 4 | 002001 | 2016-05-09 | 18.67 |
把列名改为有意义的名字,然后转为时间序列数据。
df.columns = ['code','date','close'] # 代码,日期,收盘价
df.set_index('date',inplace = True)
df.head()| code | close | |
|---|---|---|
| date | ||
| 2016-05-03 | 002001 | 20.99 |
| 2016-05-04 | 002001 | 20.42 |
| 2016-05-05 | 002001 | 20.49 |
| 2016-05-06 | 002001 | 18.70 |
| 2016-05-09 | 002001 | 18.67 |
看看都有什么股票
df.code.unique()array(['002001', '002002', '002003', '002004', '002005', '002006',
'002007', '002008', '002009', '002010', '002011', '002012',
'002013', '002014', '002015', '002016', '002017', '002018',
'002019', '002020'], dtype=object)29.4.4 绘制1只股票
要把4只股票绘制成2x2的样式,我们首先尝试绘制1只股票。
以某1只股票为例,绘制股价和10日均线:筛选数据、计算10ma、选列绘图。
# 简单移动平均
def sma(x:pd.Series, period):
return x.rolling(period).mean()
code = '002001'
tmp_df = df.query('code == @code').copy()
# tmp_df是一个独立的对象,希望和df不再产生联系
tmp_df['sma_10'] = sma(tmp_df.query('code == @code').close,10)
tmp_df[['close','sma_10']].plot()上图正式我们想要的。
要对所有股票都计算其10日MA,显然可以分组进行:
- 按股票分组,取收盘价
- 对每一组的收盘价格,应用前面的
sma()函数 - 结果写入
df['sam_10']
# 简单测试下:取子集、取close列,应用sma函数,参数是10天
df.groupby('code').close.apply(lambda x: sma(x,10)).head(15)code date
002001 2016-05-03 NaN
2016-05-04 NaN
2016-05-05 NaN
2016-05-06 NaN
2016-05-09 NaN
2016-05-10 NaN
2016-05-11 NaN
2016-05-12 NaN
2016-05-13 NaN
2016-05-16 19.652
2016-05-17 19.530
2016-05-18 19.411
2016-05-19 19.260
2016-05-20 19.324
2016-05-23 19.472
Name: close, dtype: float64# 把前面做的数据没问题吃,因此可以加入到df中
df['sma_10'] = df.groupby('code').close.apply(lambda x: sma(x,10)).values随便选1只股票来测试一下
df.query('code == "002003"')[['close','sma_10']].plot()
plt.xlabel('')
plt.legend('',frameon=False); # 图例无内容,且无边框 = 隐藏图例29.4.5 绘制2x2的子图:手动版本
注:
- 下列代码明显有很大的重复,因此必然可以改造成循环(或者列表推导式)。
- 如果你要绘制的股票有3000多个,不可能手动填写股票代码。
# 在画布上生成2x2=4个坐标系
fig, axes = plt.subplots(2, 2,figsize = (10,8), sharex=True)
# 随便拿4只股票,绘制到对应的ax上
df.query('code == "002001"')[['close','sma_10']].plot(ax=axes[0,0])
df.query('code == "002002"')[['close','sma_10']].plot(ax=axes[0,1])
df.query('code == "002003"')[['close','sma_10']].plot(ax=axes[1,0])
df.query('code == "002004"')[['close','sma_10']].plot(ax=axes[1,1]);29.4.6 绘制2x2的子图:自动版
问:已知任意4只股票的代码,绘制2x2的图形。
# 范例股票代码:
code_list = ['002001','002002','002003','002004']
# 设置画布:2行,2列,共用x轴
fig, axes = plt.subplots(2, 2,figsize = (10,8), sharex=True)
# 把2维的ndarray转为1维。 如:[[1, 2], [3, 4]] -> [1, 2, 3, 4]
# 因此,axes_1d[0]和axes[0,0],都指向左上角的坐标系。
axes_1d = axes.flatten()
# 循环这个代码列表
for i in range(len(code_list)):
code = code_list[i]
# 第i个股票代码,绘制在第i个坐标系
df.query('code == @code ')[['close','sma_10']].plot(ax=axes_1d[i])
# 去掉横轴标签,股票代码作为子图标题
axes_1d[i].set(xlabel='',title = code)
plt.subplots_adjust(hspace=0.15)我们可以把前面的内容,整理成一个函数,参数应该是:
- 数据源df
- 要绘制的4只股票的代码
# 为了节约篇幅,这里删除了注释,注释内容同前。
# 但正常情况下注释是必须的!
def plot2x2(df, code_list):
'''绘制4个股票的价格和MA
df: 全部股票的数据
code_list: 4只股票的代码
'''
fig, axes = plt.subplots(2, 2,figsize = (10,8), sharex=True)
axes_1d = axes.flatten()
for i in range(len(code_list)):
code = code_list[i]
df.query('code == @code ')[['close','sma_10']].plot(ax=axes_1d[i])
axes_1d[i].set(xlabel='',title=code)
plt.subplots_adjust(hspace=0.15)
# 随便测试4个代码
plot2x2(df, ['002003','002005','002009','002010'])把所有的股票代码取出,每4个代码成一组,分成n/4段:
all_codes = df.code.unique()
np.array_split(all_codes,len(all_codes)/4 ) # 股票代码的序列,切成4个代码一组List的List[array(['002001', '002002', '002003', '002004'], dtype=object),
array(['002005', '002006', '002007', '002008'], dtype=object),
array(['002009', '002010', '002011', '002012'], dtype=object),
array(['002013', '002014', '002015', '002016'], dtype=object),
array(['002017', '002018', '002019', '002020'], dtype=object)]简单循环上面的分段列表。显然,每一段就是4个股票代码,在循环体内调用plot2x2()即可。
# 节约篇幅,这里以前2段(8只股票)为例
for x in np.array_split(all_codes,len(all_codes)/4 )[:2]:
plot2x2(df,x)29.5 沪深300指数走势预测
(原7.6小节 p154)
29.5.1 要求
利用沪深300指数的数据,利用几个分类模型,对指数的涨跌进行预测。 需要前置章节:分类和预测。
29.5.2 数据:
index300.xlsx:沪深300指数的数据。
29.5.3 大致原理:
- 指数的k线数据,对次日涨跌进行预测。
- 如果把次日涨跌看作2种类别,则这个任务可以看成是分类预测问题
- 这本质和用叶片萼片数据判断鸢尾花的品种类似:今天走势类比叶片萼片数据,明天的涨跌类比鸢尾花的品种
- 用数据拟合一个模型,对新观测进行判断:对一朵不知品种的鸢尾花,观测叶片萼片的数据,判断(预测)其品种;对一个新的价格时间序列,观察其历史数据,判断(预测)明天的涨跌。
- 或者说把价格走势数据分成2类:明天会涨/明天会跌,对新的数据预测其类别。
数据读取和清洗
df = pd.read_excel('data/case7.6/index300.xlsx')
df.head()| Indexcd | Idxtrd01 | Idxtrd02 | Idxtrd03 | Idxtrd04 | Idxtrd05 | Idxtrd06 | Idxtrd07 | Idxtrd08 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 300 | 2014-01-02 | 2323.43 | 2325.99 | 2310.65 | 2321.98 | 451942.91 | 4901221.11 | -0.3454 |
| 1 | 300 | 2014-01-03 | 2311.97 | 2314.84 | 2280.89 | 2290.78 | 597826.45 | 5773970.99 | -1.3436 |
| 2 | 300 | 2014-01-06 | 2286.37 | 2286.37 | 2229.33 | 2238.64 | 663004.03 | 5997936.01 | -2.2762 |
| 3 | 300 | 2014-01-07 | 2222.31 | 2246.79 | 2218.65 | 2238.00 | 437531.03 | 4256564.81 | -0.0284 |
| 4 | 300 | 2014-01-08 | 2240.64 | 2262.58 | 2228.42 | 2241.91 | 513488.54 | 5069148.89 | 0.1747 |
改个合理的列名,转为时间序列格式。
df.columns = ['code','date','open','high','low','close','vol','xxx','ret'] # 倒数第二列不知道是什么
df.set_index('date',inplace=True)
df.tail()| code | open | high | low | close | vol | xxx | ret | |
|---|---|---|---|---|---|---|---|---|
| date | ||||||||
| 2014-12-25 | 300 | 3254.48 | 3335.78 | 3226.32 | 3335.42 | 3097995.47 | 33012893.99 | 3.2514 |
| 2014-12-26 | 300 | 3343.64 | 3453.34 | 3335.01 | 3445.84 | 3846141.24 | 43883842.71 | 3.3105 |
| 2014-12-29 | 300 | 3502.18 | 3524.28 | 3405.84 | 3455.46 | 4250150.37 | 50500450.84 | 0.2791 |
| 2014-12-30 | 300 | 3450.81 | 3491.83 | 3422.17 | 3457.55 | 3282338.73 | 39460777.24 | 0.0607 |
| 2014-12-31 | 300 | 3462.39 | 3542.34 | 3452.50 | 3533.71 | 3459347.60 | 40371088.81 | 2.2025 |
这个案例中,使用如下信息来进行分类(预测明天走势,见变量注释)
def sma(x:pd.Series, period):
return x.rolling(period).mean()
# 收盘价的10日均线
ma10 = sma(df.close,10)
A1 = df.close / ma10 # 收盘价相对10日均线
A2 = df.vol / sma(df.vol,10) # 成交量相对10日成交量的均值
A3 = df.ret # 回报率
A4 = df.high / ma10 # 最高价相对10日均线
A5 = df.low / ma10 # 最低价相对10日均线
A6 = df.high - df.low # 最高价和最低价之差
A7 = df.close - df.open # 收盘价相对开盘价
data = pd.concat([A1,A2,A3,A4,A5,A6,A7],axis=1)
data.columns = ['A' + str(i) for i in range(1,8)]
data.tail()| A1 | A2 | A3 | A4 | A5 | A6 | A7 | |
|---|---|---|---|---|---|---|---|
| date | |||||||
| 2014-12-25 | 1.008022 | 0.834703 | 3.2514 | 1.008131 | 0.975050 | 109.46 | 80.94 |
| 2014-12-26 | 1.033503 | 1.013465 | 3.3105 | 1.035752 | 1.000262 | 118.33 | 102.20 |
| 2014-12-29 | 1.029035 | 1.081501 | 0.2791 | 1.049530 | 1.014258 | 118.44 | -46.72 |
| 2014-12-30 | 1.024952 | 0.841631 | 0.0607 | 1.035114 | 1.014464 | 69.66 | 6.74 |
| 2014-12-31 | 1.042181 | 0.910890 | 2.2025 | 1.044726 | 1.018230 | 89.84 | 71.32 |
模型要拟合的结果,是“明天的涨跌”:
df.ret是今天的涨跌幅度,判断是否大于0(今天的涨跌),再取一阶提前shift(-1)(明天的涨跌)- 去掉缺失值。
data['y'] = ((df.ret > 0)*1).shift(-1) # 明天的涨跌
data.tail() # 看看最后一行是不是NA| A1 | A2 | A3 | A4 | A5 | A6 | A7 | y | |
|---|---|---|---|---|---|---|---|---|
| date | ||||||||
| 2014-12-25 | 1.008022 | 0.834703 | 3.2514 | 1.008131 | 0.975050 | 109.46 | 80.94 | 1.0 |
| 2014-12-26 | 1.033503 | 1.013465 | 3.3105 | 1.035752 | 1.000262 | 118.33 | 102.20 | 1.0 |
| 2014-12-29 | 1.029035 | 1.081501 | 0.2791 | 1.049530 | 1.014258 | 118.44 | -46.72 | 1.0 |
| 2014-12-30 | 1.024952 | 0.841631 | 0.0607 | 1.035114 | 1.014464 | 69.66 | 6.74 | 1.0 |
| 2014-12-31 | 1.042181 | 0.910890 | 2.2025 | 1.044726 | 1.018230 | 89.84 | 71.32 | NaN |
在一个序列进行了滞后/提前运算之后,检查一下开头和结尾:
- 要用今天的信息,预测明天的涨跌,那么数据最后一天必然没有明天的涨跌信息的。看y的末尾是否为NA。
- 同理,如果是做了滞后运算,最好看一样第一天的数据是否为NA。
29.5.4 模型的拟合与预测
把数据成4份:
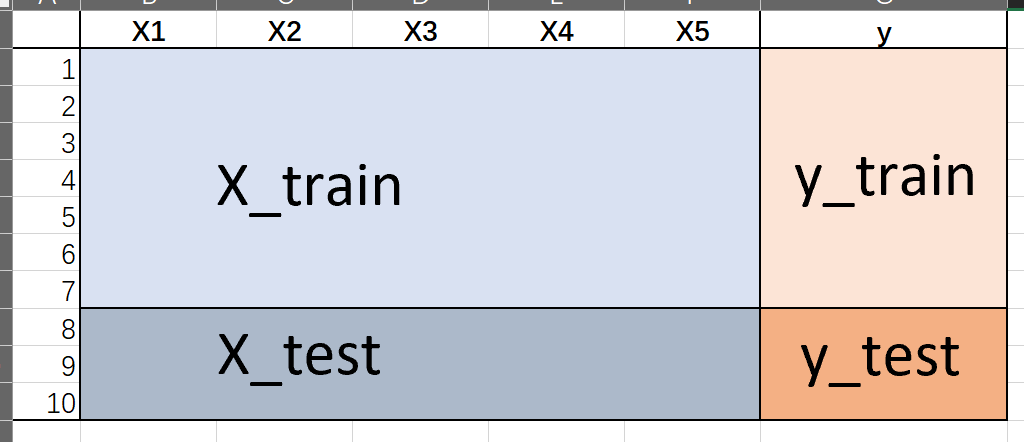
数据本身由2个部分组成:(X是大写,表示矩阵;y是小写,表示向量)
- X:信息特征(影响涨跌的因素),即A1-A7
- y:二元标签(明天的涨跌)
把上述2个数据,前后截断。前半截数据用来训练模型:
- X_train:训练模型用的特征信息
- y_train:训练模型用的二元标签
后半截数据用来对模型进行样本外预测:
- X_test:新的特征信息,用上面生成的模型预测明天的涨跌pred_test
- y_train:把预测值pred_dest和真实的涨跌对比,衡量模型样本外的预测能力。
我们可以用对test数据的预测,来判断模型(或者特定参数)的预测准确性。
data.dropna(inplace = True)
X = data.drop('y',axis=1)
y = data['y']
test_size = X.shape[0]//6
print(f"{test_size=}")
X_train = X[:-test_size].copy()
y_train = y[:-test_size].copy()
assert len(X_train) == len(y_train)
X_test = X.iloc[-test_size:].copy()
y_test = y.iloc[-test_size:].copy()
assert len(X_test) == len(y_test)test_size=39训练模型,再用测试数据进行预测测试:以Logistic模型为例:
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
model = LogisticRegression() # 使用Logistic模型
model.fit(X_train,y_train) # 用训练数据拟合模型
pred_train = model.predict(X_train) # 用训练好的模型,对训练数据进行预测
pred_test = model.predict(X_test) # 用训练好的模型,对测试数据进行预测
acc_train = (y_train == pred_train).mean() # 训练数据的准确率
acc_test = (y_test == pred_test).mean() # 测试数据的准确率
print(f'model: {type(model).__name__}, {acc_train=:.2f}, {acc_test=:.2f}')model: LogisticRegression, acc_train=0.58, acc_test=0.72注意,X_test 是“新数据”,我们假装不知道真实的结果。
对于任何新的数据,要做预测(进行分类),只要model.predict(X_test)即可
pred_test = model.predict(X_test)
pred_test # 显示预测值array([1., 1., 1., 1., 1., 1., 0., 1., 1., 0., 0., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1.])X_test_with_pred = X_test.copy()
X_test_with_pred['pred'] = pred_test
X_test_with_pred.tail()| A1 | A2 | A3 | A4 | A5 | A6 | A7 | pred | |
|---|---|---|---|---|---|---|---|---|
| date | ||||||||
| 2014-12-24 | 0.980798 | 0.842313 | -2.8433 | 1.014186 | 0.968079 | 151.86 | -101.76 | 1.0 |
| 2014-12-25 | 1.008022 | 0.834703 | 3.2514 | 1.008131 | 0.975050 | 109.46 | 80.94 | 1.0 |
| 2014-12-26 | 1.033503 | 1.013465 | 3.3105 | 1.035752 | 1.000262 | 118.33 | 102.20 | 1.0 |
| 2014-12-29 | 1.029035 | 1.081501 | 0.2791 | 1.049530 | 1.014258 | 118.44 | -46.72 | 1.0 |
| 2014-12-30 | 1.024952 | 0.841631 | 0.0607 | 1.035114 | 1.014464 | 69.66 | 6.74 | 1.0 |
因此,如果你有新的数据,同样构造一个类似结构DF,然后调用model.predict()即可。
比较3种模型:LogisticRegression,SVC,MLPClassifier(具体原理不展开)
不同的模型有完全相同的接口,因此可以写成函数,以使用何种模型作为参数。
def do_test(model):
model.fit(X_train,y_train) # 用训练数据拟合模型
pred_train = model.predict(X_train) # 用训练好的模型,对训练数据进行预测
pred_test = model.predict(X_test) # 用训练好的模型,对测试数据进行预测
acc_train = (y_train == pred_train).mean() # 训练数据的准确率
acc_test = (y_test == pred_test).mean() # 测试数据的准确率
print(f'model: {type(model).__name__} \n\t {acc_train=:.2f}, {acc_test=:.2f}')
do_test(LogisticRegression())
do_test(SVC(kernel='rbf'))
do_test(MLPClassifier(solver='lbfgs',alpha=1e-5,hidden_layer_sizes=(5,2),random_state=1))model: LogisticRegression
acc_train=0.58, acc_test=0.72
model: SVC
acc_train=0.58, acc_test=0.72
model: MLPClassifier
acc_train=0.52, acc_test=0.69可以看到3个模型的样本外预测的能力。
29.6 基于主成分聚类的上市公司盈利能力分析
(原7.7小节 p157)
需要前置章节:因子分析、聚类
29.6.1 快速回顾:主成分和K-means聚类
主成分
主要用于降维,缩减变量的数据,或者说把样本的某些高度相关的属性合并,但又不希望损失太多信息。
一个极端的例子:如果\(x_1,x_2\)相关性达到0.99,那么可以认为他们几乎表示相同的信息,即使把这2个变量用某种方法变成1个(比如求平均或者直接去掉一个),显然不会有什么损失。
例如:同学成绩 \([语文,英语,数学,物理]\),有4个变量。按主成分分析,(可能)可以把4个变量合成2个变量(2个主成分)。如
\[ x_1 = a * 语文 + b * 英语 \] \[ x_2 = c * 数学 + c * 物理 \] (显然这是2个线性回归)
那么我们用2个变量 \([x_1, x_2]\),来表达原来4个变量所表达的大部分信息(多少算大部分?80?90%?由你决定)。
这个计算的过程是自动的,每个主成份由什么因素构成,其实是电脑计算的结果。
如果计算的结果,确实是\(x_1\)中语文和英语占了大部分(但数学和物理的系数一般不是0),\(x_2\)中数学和物理占了大部分(语文和英语的系数一般也不是0),那么我们可以考虑称\(x_1\)为“文科”,\(x_2\)为“理科”。
变量由多变少,就是所谓降维,往往极大地加快矩阵运算的速度。并且主成分往往是有意义的(如文科、理科),这对我们进行其他分析可能有帮助。
当然,如果变量之间没什么关联性,那么这一切也无从谈起了。
K-means聚类
把样本,按他们各个变量之间的“距离”进行归类,但需要由你指定分成多少类。
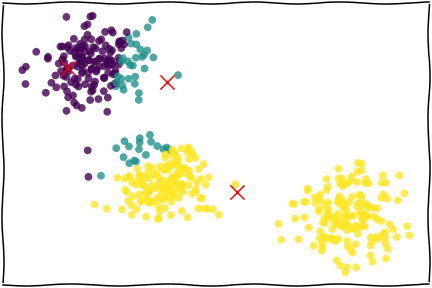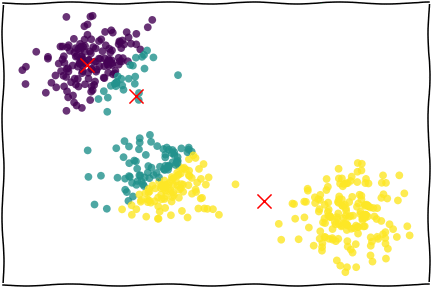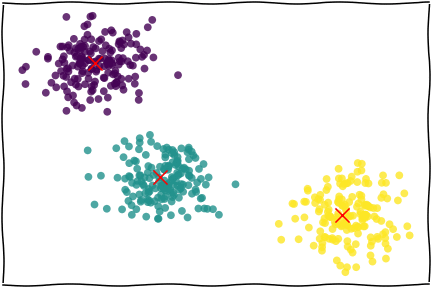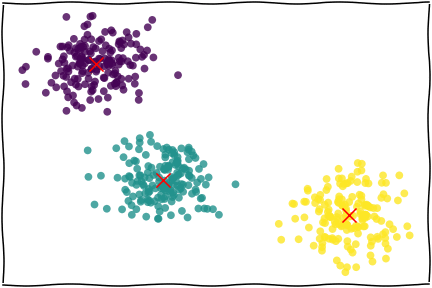
图片来自 Applied Data Analysis in Python
基本原理:
- 给定K个聚类数量(要分K类)
- 确定每个聚类的初始中心(也可以让Python自己定)
- 对于所有的点,计算到K个中心点的距离(欧氏距离),划分到最近的一个点,构成一组。(这么多个中心,最靠近哪个中心,就算进那一组)
- 迭代:对于上述过程中划分好的K个类别,重新计算新的中心点(均值),再次进行最邻近的划分,重复这个过程N次。
一个迭代2轮的示例:
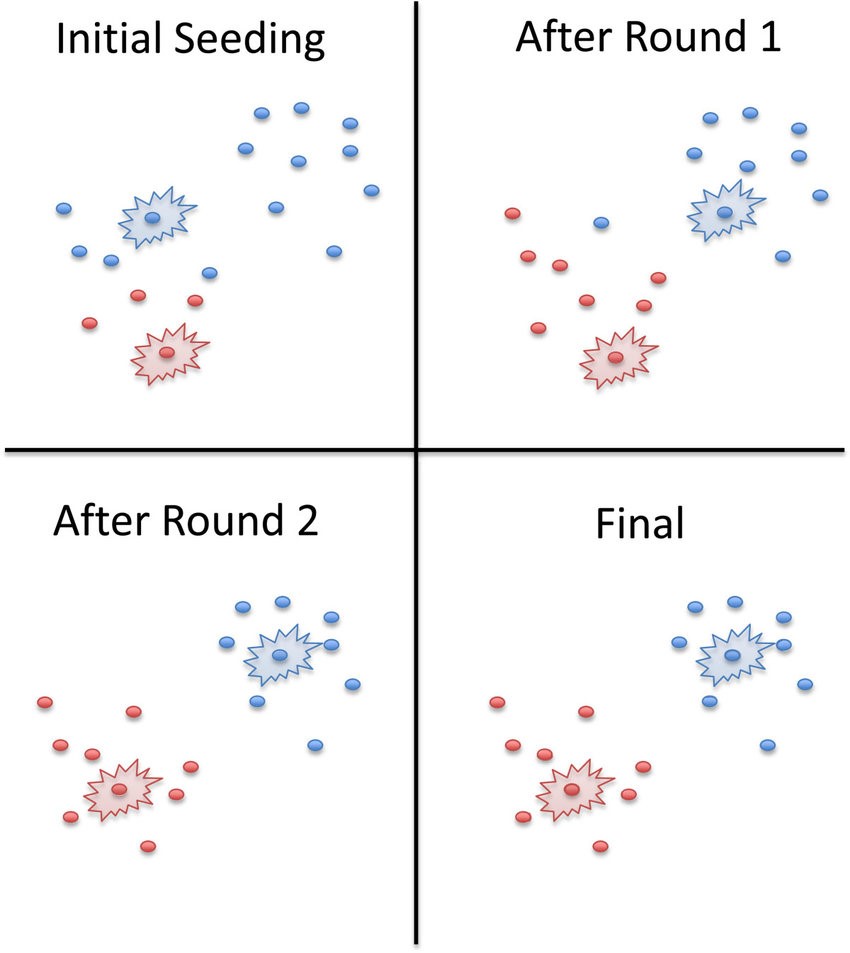
但要注意:这完全是一个“亲疏远近”的分类方法:相近的就会被归为一类,本身没有“好坏”的含义。但其中的指标可能有好坏,这需要分类后判断。
29.6.2 要求
- 对于计算机行业的公司,对其财务数据进行降维,用k-means聚类,再计算每一类的利润增长率,以判断计算机行业中不同公司的水平层次。
数据:
财务指标数据.xlsx申万行业分类
29.6.3 原理和实现
- 对上市公司的一系列数据的进行降维。
- 对降维后的数据进行K-means聚类,分出4类。
- 计算每一类的利润增长率,进而判断每一类的优劣。
注意:对财务报表的指标进行进行k-means聚类可能不是一个好的做法,因为同一个行业里的公司,他们经营业绩往往是连续分布的,而不是“扎堆分布”的。而k-means聚类是一个基于距离的算法,能够把各自聚集的样本分开来,但是对连续分布的样本可能没什么办法。
29.6.4 读取数据
# 读取财务指标
# 其中的指标的含义见教材p157-p158,但暂时不重要
df = pd.read_excel('data/case7.7/财务指标数据.xlsx',
converters = {'Stkcd':str,'Accper':pd.to_datetime})
df.round(4).head()| Stkcd | Accper | F050502B | F050102B | F050202B | F051201B | F051501B | F053301B | F051401B | F052101B | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 000667 | 2015-12-31 | 0.0725 | 0.0306 | 0.0255 | 0.0453 | 0.0908 | 0.2879 | 0.1257 | 0.1607 |
| 1 | 000838 | 2015-12-31 | 0.0755 | 0.0206 | 0.0196 | 0.0257 | 0.1161 | 0.3483 | 0.0666 | 0.1125 |
| 2 | 600816 | 2015-12-31 | 0.4245 | 0.2844 | 0.2844 | 0.1880 | 0.6665 | NaN | 0.8924 | NaN |
| 3 | 600358 | 2015-12-31 | 0.0422 | 0.0475 | 0.0176 | 0.0514 | 0.1459 | 0.8675 | 0.3936 | 0.2412 |
| 4 | 601155 | 2015-12-31 | 0.1837 | 0.0426 | 0.0404 | 0.0936 | 0.1018 | 0.2681 | 0.1388 | 0.1728 |
df.Accper.unique() # 只有1天,因此日期是非必须的<DatetimeArray>
['2015-12-31 00:00:00']
Length: 1, dtype: datetime64[ns]df.Stkcd.unique().shape # 接近3000只股票(2842,)读取行业分类
ind_info_df = pd.read_excel('data/case7.7/申万行业分类.xlsx',
converters={'股票代码':str})
ind_info_df| 行业名称 | 股票代码 | 股票名称 | 起始日期 | 结束日期 | |
|---|---|---|---|---|---|
| 0 | 采掘 | 000552 | 靖远煤电 | 2008-06-02 00:00:00 | NaN |
| 1 | 采掘 | 000571 | 新大洲A | 2011-10-10 00:00:00 | NaN |
| 2 | 采掘 | 000629 | 攀钢钒钛 | 2015-10-31 00:00:00 | NaN |
| 3 | 采掘 | 000655 | *ST金岭 | 2015-10-31 00:00:00 | NaN |
| 4 | 采掘 | 000723 | 美锦能源 | 2008-06-02 00:00:00 | NaN |
| ... | ... | ... | ... | ... | ... |
| 3566 | 综合 | 600817 | ST宏盛 | 2016-08-04 01:33:00 | NaN |
| 3567 | 综合 | 600818 | 中路股份 | 2015-08-04 00:00:00 | NaN |
| 3568 | 综合 | 601992 | 金隅集团 | 2017-06-29 00:00:00 | NaN |
| 3569 | 综合 | 603060 | 国检集团 | 2016-11-06 18:27:00 | NaN |
| 3570 | 综合 | 603183 | 建研院 | 2017-08-26 09:17:00 | NaN |
3571 rows × 5 columns
按股票代码merge,去掉na,去掉日期,重置index,最终获得我们要的数据:计算机板块中的每一只股票和它的8个指标。
(这部分的操作请回忆我们的作业)
我们的任务,就是利用这8个指标,对股票进行K-means聚类。
data = pd.merge(df, ind_info_df.iloc[:, :3], left_on='Stkcd',
right_on='股票代码').query('行业名称 == "计算机"').dropna().drop(['Accper', 'Stkcd', '行业名称'], axis=1).reset_index(drop=True)
data.head()| F050502B | F050102B | F050202B | F051201B | F051501B | F053301B | F051401B | F052101B | 股票代码 | 股票名称 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.321397 | 0.228925 | 0.227827 | 0.188137 | 0.474756 | 0.715053 | 0.557304 | 1.357928 | 002280 | 联络互动 |
| 1 | 0.154194 | 0.091206 | 0.093423 | 0.120079 | 0.154341 | 0.434843 | 0.136904 | 0.210119 | 300271 | 华宇软件 |
| 2 | 0.106211 | 0.076708 | 0.071280 | 0.077224 | 0.117922 | 0.499746 | 0.131880 | 0.180142 | 300324 | 旋极信息 |
| 3 | 0.083760 | 0.058820 | 0.064392 | 0.055300 | 0.174578 | 0.488951 | 0.119061 | 0.212990 | 002230 | 科大讯飞 |
| 4 | 0.184059 | 0.112991 | 0.102916 | 0.096451 | 0.265636 | 0.562932 | 0.244306 | 0.403114 | 300367 | 东方网力 |
先把股票的代码和名称,以及8个指标分开。
code_name = data.iloc[:,-2:]
code_name.head()| 股票代码 | 股票名称 | |
|---|---|---|
| 0 | 002280 | 联络互动 |
| 1 | 300271 | 华宇软件 |
| 2 | 300324 | 旋极信息 |
| 3 | 002230 | 科大讯飞 |
| 4 | 300367 | 东方网力 |
X = data.iloc[:,:-2]
X.shape(154, 8)对于上述X
- 保留所有大于0的值(等价于把小于0的值标记为NA):
X[X>0] - 对于每个属性,去掉8倍以上的观测值。
- 去掉所有包含NA的行:等于去掉原数据中有缺失值的行、有小于0的值的行、以及有属性大于均值8倍的行。
X = X[X>0]
assert all(X>0)
X = X.apply(lambda c: c[c<8*c.mean()])
X = X.dropna()
X.shape(130, 8)只剩下130个样本了。
29.6.5 归一化和主成分分析
先进行归一化:对于8个指标,在每一个指标中(每一列中),我们把指标值映射到0到1之间(最低者为0,最高者为1,其他值按比例排在其中)。
确保每一列从0到1分布。
from sklearn.preprocessing import MinMaxScaler
from sklearn.decomposition import PCA
mms = MinMaxScaler()
X2 = mms.fit_transform(X)对X2进行归一化之后,可以进行主成分分析,要求提取3个主成分(8个变量要求缩减到3个)
注意:参数n_components是你要提取几个主成分的意思。
pca = PCA(n_components=3) # 提取3个主成分
Y = pca.fit_transform(X2) # 获得新的数据
Y.shape(130, 3)依然是130个样本,8个变量缩减3个。
Y[:5]array([[ 1.90412959, 0.08066129, -0.39295183],
[ 0.27675405, -0.16340431, 0.08202221],
[ 0.03642993, 0.02642522, 0.08086289],
[-0.04285748, 0.15449534, -0.0091774 ],
[ 0.53442846, 0.07900558, -0.07085411]])查看特征向量
pca.components_array([[ 3.58255463e-01, 3.77691621e-01, 4.02468928e-01,
4.33683168e-01, 3.74982333e-01, 2.69608274e-01,
3.20458085e-01, 2.50890372e-01],
[-3.59350970e-01, -1.89711676e-01, -1.43431475e-01,
-4.05273047e-01, 3.45833039e-01, 6.58048499e-01,
2.33127415e-01, 2.07559198e-01],
[ 6.72839854e-02, 2.12912321e-02, -5.80726287e-04,
3.20028729e-01, -3.32783213e-01, 6.80068064e-01,
-4.71299118e-01, -3.11834454e-01]])查看每个主成分的贡献率和总的贡献率
pca.explained_variance_ratio_array([0.67847685, 0.20913697, 0.07212103])sum(pca.explained_variance_ratio_)0.9597348490623552第一个主成分包含了原数据68%左右的信息,第二个包含了21%左右,第三个包含了7.2%左右,合计解释了96%的信息。
等于说,我们用3个变量,就涵盖了原来8个变量96%的信息。
(见参考教材p160-p161,这几个数字与教材相同。)
我们把提取的3个主成分绘制成3d图形
Y_df = pd.DataFrame(Y)
Y_df.columns = ['y1','y2','y3']
Y_df.head()| y1 | y2 | y3 | |
|---|---|---|---|
| 0 | 1.904130 | 0.080661 | -0.392952 |
| 1 | 0.276754 | -0.163404 | 0.082022 |
| 2 | 0.036430 | 0.026425 | 0.080863 |
| 3 | -0.042857 | 0.154495 | -0.009177 |
| 4 | 0.534428 | 0.079006 | -0.070854 |
import plotly.express as px
fig = px.scatter_3d(Y_df, x='y1', y='y2', z='y3', opacity=0.7)
fig.show()从任何一个角度看,计算机上市公司的财务数据,并没有显示出“分类聚集”的情况(见快速回顾的图),因此k-means来进行分析,可能不是一个好主意。
29.6.6 k-means聚类分析
虽然可能不是个好办法,但是过程还是可以做一下。
from sklearn.cluster import KMeans
# 创建一个k-means模型,要求
# 分成5类,初始状态是0(这个不用管),最大循环次数1000次
model = KMeans(n_clusters=5,random_state=0,max_iter=1000)
# 用这个模型对主成分数据进行分类
model.fit(Y)
# 查看分类的结果
model.labels_array([3, 4, 0, 0, 3, 0, 1, 2, 0, 4, 2, 2, 4, 4, 2, 1, 1, 2, 2, 0, 0, 4,
2, 0, 1, 1, 4, 1, 3, 2, 2, 4, 1, 4, 2, 2, 2, 0, 1, 3, 0, 0, 2, 2,
4, 0, 0, 2, 4, 0, 0, 0, 0, 1, 0, 1, 1, 0, 2, 4, 2, 4, 1, 0, 3, 1,
1, 1, 1, 0, 2, 0, 4, 2, 2, 0, 0, 0, 0, 1, 4, 4, 3, 2, 2, 4, 4, 3,
0, 0, 0, 2, 4, 2, 3, 2, 3, 4, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 1, 1,
0, 2, 1, 0, 4, 3, 3, 4, 1, 2, 1, 2, 3, 1, 0, 1, 1, 4, 2, 2],
dtype=int32)把分组信息合并到我们前面保留的代码和股票简称数据中。
result = pd.concat([code_name, pd.Series(model.labels_,name='分组')],axis=1)
result[result.分组==2].head(10)| 股票代码 | 股票名称 | 分组 | |
|---|---|---|---|
| 7 | 002649 | 博彦科技 | 2.0 |
| 10 | 600571 | 信雅达 | 2.0 |
| 11 | 002530 | 金财互联 | 2.0 |
| 14 | 300253 | 卫宁健康 | 2.0 |
| 17 | 603019 | 中科曙光 | 2.0 |
| 18 | 600845 | 宝信软件 | 2.0 |
| 22 | 300339 | 润和软件 | 2.0 |
| 29 | 300469 | 信息发展 | 2.0 |
| 30 | 300229 | 拓尔思 | 2.0 |
| 34 | 300479 | 神思电子 | 2.0 |
整理一下数据
result_km = result.groupby('分组')['股票名称'].agg(lambda x:', '.join(x)).reset_index()
result_km| 分组 | 股票名称 | |
|---|---|---|
| 0 | 0.0 | 旋极信息, 科大讯飞, 辉煌科技, 云赛智联, 川大智胜, 航天长峰, 广电运通, 易华录,... |
| 1 | 1.0 | 神州数码, 汉王科技, 南天信息, 合众思壮, 超图软件, 佳都科技, 海兰信, 华胜天成,... |
| 2 | 2.0 | 博彦科技, 信雅达, 金财互联, 卫宁健康, 中科曙光, 宝信软件, 润和软件, 信息发展,... |
| 3 | 3.0 | 联络互动, 东方网力, 飞天诚信, 同花顺, 银江股份, 御银股份, 数字政通, 捷成股份,... |
| 4 | 4.0 | 华宇软件, 天玑科技, 皖通科技, 恒华科技, 世纪瑞尔, 太极股份, 中海达, 天源迪科,... |
# 查看第2组的股票
print(result_km.iloc[2,1])博彦科技, 信雅达, 金财互联, 卫宁健康, 中科曙光, 宝信软件, 润和软件, 信息发展, 拓尔思, 神思电子, 浪潮信息, 银信科技, 赛为智能, 恒生电子, 浩丰科技, 广联达, 石基信息, 天泽信息, 新大陆, 新国都, ST中安, 启明星辰, 四维图新, 东方国信, 聚龙股份, *ST工新, 四方精创, 万达信息, 凯瑞德, 湘邮科技29.6.7 每一组的股票的平均利润增长率
分组计算每一组的股票15年的利润增长率的均值,难度低于作业03,可以作为练习。