19 Plus: 统计知识小复习
19.1 均值和中位数
- 均值mean:
\[\overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}\]
中位数median:一半的样本大于中位数,一半的样本小于中位数
众数mode:出现次数最多的值
注意:
均值容易受到极端值的影响(我们班同学和马云平均几十亿身价):因此很多分析(如做计量),要考虑是否要去掉极端值,或者截尾(如去掉头尾某个百分比的数据)。
中位数不会被极端值拉偏:(1,2,3,4,5)的中位数是3;(1,2,3,4,一个亿)的中位数还是3。
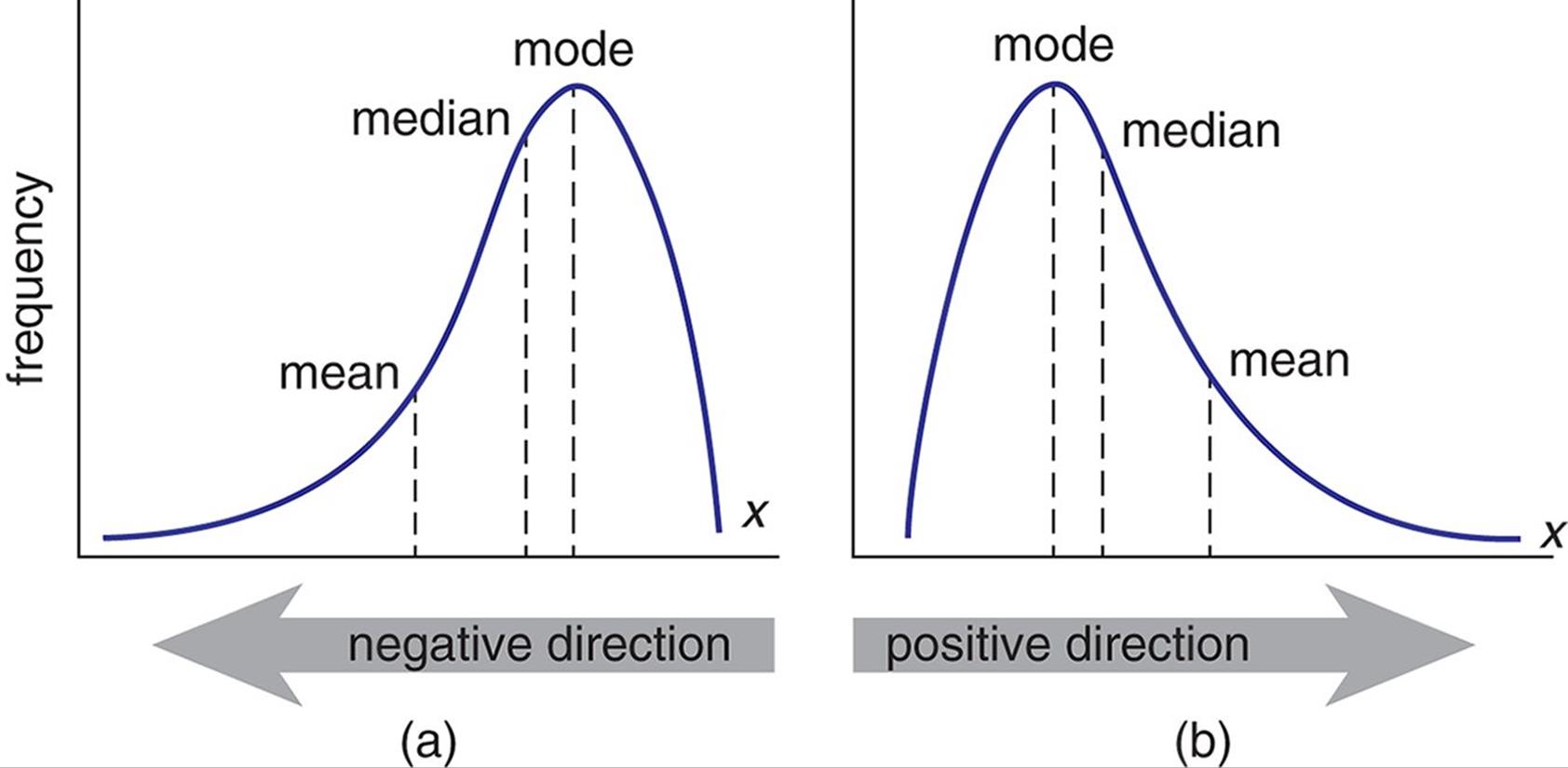
如果一个分布非常右偏:存在数量很少,但值很大的样本(例如上市公司的总资产,个人的收入等),中位数会小于均值。同时观察中位数和均值能更好地认识数据。
19.2 样本均值和标准误
总体均值往往难以获得:我们想知道全中国人的14亿人的平均体重,但这几乎是不可能的。
但求一个样本均值就比较容易获得:比如在某家医院体检的数据中求平均体重。
样本均值,是我们的对总体均值的一个猜测(更正式称之为”估计”)。
问题:我们用样本均值来估计总体均值,我们猜得有多准?
如:从一家医院的体检数据得到的平均体重,能代表全中国人的平均体重吗?
如:这家医院的体检数据中算出的平均体重,和另一家医院体检数据中算出的平均体重,谁更有代表性?
19.2.1 标准误的概念:我们猜得有多准?
抽样本身是随机的。同样的抽样方法,每一次抽样所获得的样本会不同。
比如:同一家医院,今天的体检者,和明天的体检者,显然是两批不同的人。
这两批人,可以视为从”中国人”这个总体中,进行了2次抽样。
注意:同一天体检的人不是完全随机的,可能有”自选择”的问题,这里先不考虑。
因为抽样得到的样本是随机的,因此,从样本计算的均值,也是一个随机变量:样本均值是一个随机变量。
- 今天体检者的平均体重,和明天体检者的平均体重
假定样本的数量为n
- 体检中心每天只能接待n个体检者
那么样本均值(m天,每天内体检者的平均体重),会服从一个正态分布
\[\overline{X}\sim N\left( \mu,\frac{\sigma^{2}}{n} \right)\]
其中:
\(\mu\)是总体均值
- 全中国14亿人的平均体重
\(\sigma^{2}\)是总体的方差
- 全中国14亿人的体重的方差
样本均值是一个围绕总体均值的随机变量
某次抽样的样本均值大一点,某次抽样的样本均值小一点
但总的来说,样本均值围绕在总体均值附近(正态分布的形状)
我们的猜测有多准?样本均值,是比较集中于总体均值附近,还是比较分散?
样本均值的方差是\(\frac{\sigma^{2}}{n}\),样本均值的标准差为\(\frac{\sigma}{\sqrt{n}}\)
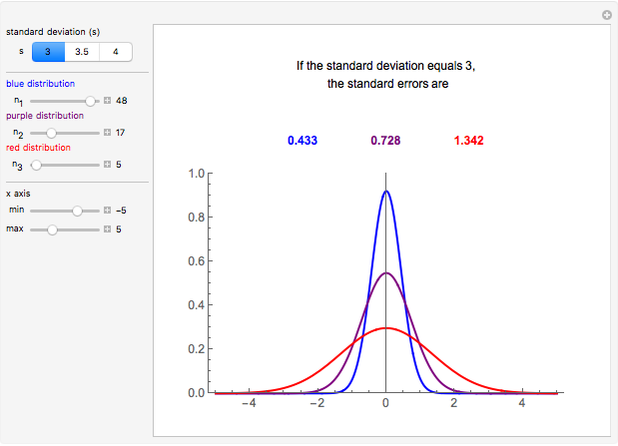
可见,你抽样的样本n越大,样本均值的方差越小。你的样本均值(你对总体均值的猜测)就猜得越准确(很可能落在很靠近总体均值的某个位置)
图:标准差=3,样本数为5,17和48时的标准误。
问题是,我只知道样本数量n,但不知道总体方差\(\sigma^{2}\)和总体标准差\(\sigma\)
\(\overline{X}\sim N\left( \mu,\frac{\sigma^{2}}{n} \right)\)
想知道14亿人的体重的方差,就等于要知道14亿人的体重。
我们用样本均值来估计总体均值,也会用样本标准差\(S\)来估计总体标准差\(\sigma\)
因此:令样本标准差为\(S\),替代\(\frac{\sigma}{\sqrt{n}}\)中的\(\sigma\),就得到”均值标准误”:
\[S.E.\ of\ Mean = \ \frac{S}{\sqrt{n}}\]
均值标准误是:我们的对样本均值和总体均值之间的平均差异程度的估计
通俗地讲:均值标准误衡量的是,我们用样本均值来估计总体均值,这个估计可能有多准确?
或者说:我们这个样本均值,可能落在总体均值的附近,是可能比较近,还是可能没那么近?
19.2.2 自举法(Bootstrap)
对于全国14亿人,假定你有1000个样本。你要估计全国人的平均体重。
对这1000个体重的样本,进行”放回抽样”,抽1000次,计算其均值。
抽一个人,放回,再抽一个人,重复1000次。
注:因为是放回抽样,极有可能里面有重复的样本。
重复上面的过程M次,例如500次。可以得到500个均值。
对500个均值再求均值,这是我们的对总体均值的估计值。
对500个均值求标准差,就可以得到均值标准误(同前),也可以求置信区间等等。
Bootstrapping Statistics. What it is and why it’s used. | by Trist'n Joseph | Towards Data Science
19.3 方差和样本方差
方差(总体方差):总体的数量是N
\[\sigma^{2} = \frac{1}{N}\sum_{i = 0}^{n}\left( X_{i} - \mu \right)^{2}\]
\[\ \]
样本方差:在数量为N的总体中,抽取了n个样本
\[S^{2} = \frac{1}{n - 1}\sum_{i = 0}^{n}\left( X_{i} - \overline{X} \right)^{2}\]
样本方差\(S^{2}\)是总体方差\(\sigma^{2}\)的无偏估计量,但注意\(S^{2}\)的分母是\(n - 1\),统计和计量软件计算方差,一般默认是用\(S^{2}\)
一般的软件默认你的数据只是一个”样本”,而你想值得是”总体”的信息。
19.4 偏度Skewness和峰度Kurtosis
19.4.1 偏度
描述变量的分布是否对称的统计量。
\[Skewness = \frac{1}{(n - 1)S^{3}}\sum_{i = 0}^{n}\left( X_{i} - \overline{X} \right)^{3}\]
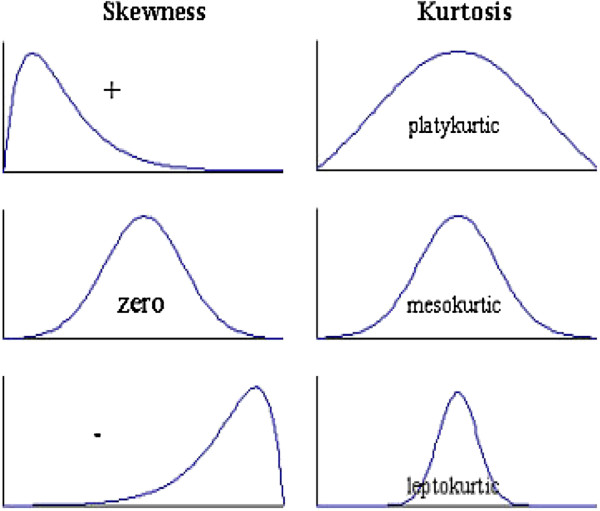
偏度为0,则分布左右对称
偏度为正,成为右偏或者正偏:在分布的右侧有一段长尾:
例如个人的财富:有极少数人,拥有极多的财富。
很多情况下,和钱有关的变量,都可能是右偏分布。
如果做计量,可以考虑对这些变量取对数:实践中,人或者公司的收入、财富、资产等等,一般也是要取对数的。
偏度为负数,成为左偏或者负偏。
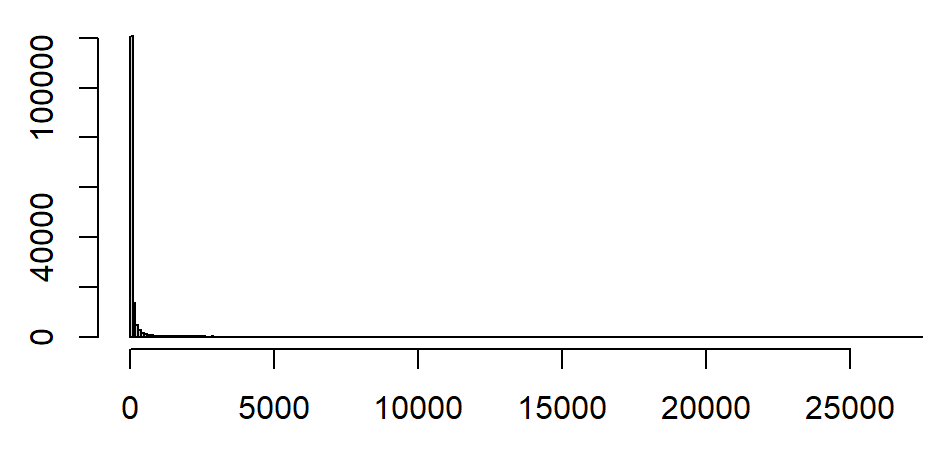
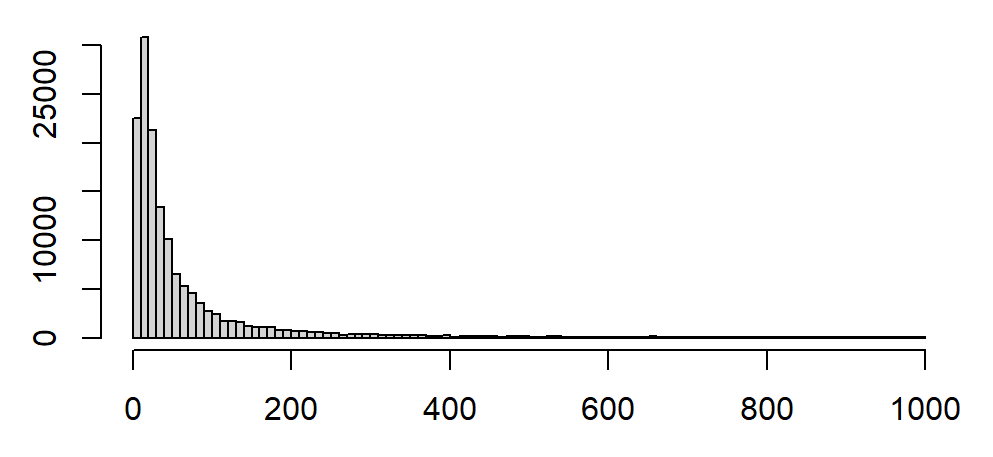
例:部分上市公司的多年年报的总资产分布(亿)
非常右偏,右侧有极长的长尾。
局部放大,只看(0,1000)
19.4.2 峰度
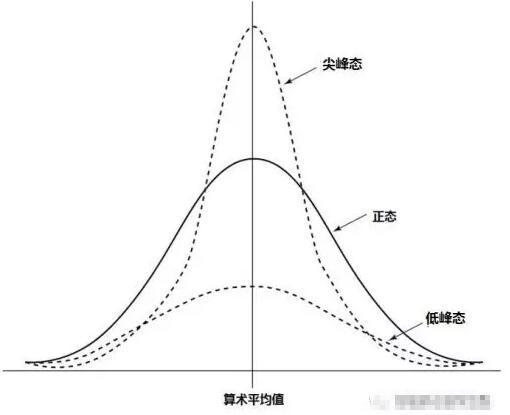
峰度:描述一个分布是陡峭还是平缓。
\[Kurtosis = \frac{1}{(n - 1)S^{4}}\sum_{i = 0}^{n}{\left( X_{i} - \overline{X} \right)^{4} - 3}\]
SPSS中,公式的最后有”-3”:峰度值接近0,则分布的陡峭程度接近正态分布
大于0,则分布更陡峭:尖峰分布;小于0,分布更平缓:平峰分布。
19.5 统计检验
统计检验:判断数据是否支持某个假设。
一般来说,我们会提出一个关于总体的假设(例如“这批产品质量符合标准”,这种药物有显著的疗效
,学历更高则收入更高
),然后根据样本数据来推断这个假设是否成立。
多数问题都可以总结为:2组/多组样本之间有没有差异
,或者“1组样本和假设值/理论值之间有没有差异”。
参数检验 vs 非参数检验
参数检验:假定总体服从某种分布(比如人的身高服从正态分布),然后我们用样本来推断总体的参数(正态分布有2个参数:均值和方差)。例如:
- t检验:如根据样本均值和标准差,判断两个总体均值是否相等。
- 方差分析:用于比较三个或以上组的均值是否有显著差异。
- 卡方检验:用于测试观测值与理论值之间的差异。
非参数检验:非参数检验不依赖于总体分布的假设,通常用于对数据的分布或形状没有明确的先验假设的情况下。例如:
- Wilcoxon秩和检验:用于比较两个相关或配对的样本中位数是否相等。
- Kruskal-Wallis H检验:用于比较三个或以上组的中位数是否有显著差异。
- Mann-Whitney U检验:用于比较两个不相关的样本中位数是否相等,适用于小样本或非正态数据。
19.6 t检验:预备
回忆前文:
- 样本均值,均值的抽样分布:样本均值是一个随机变量:
样本均值服从正态分布:
\[\overline{X}\sim N\left( \mu,\frac{\sigma^{2}}{n} \right)\]
标准化:
\[Z = \frac{\overline{X} - \mu}{\sqrt{\frac{\sigma^{2}}{n}}}\]
Z服从标准正态分布。
因此,我们可以计算,我们手中的样本均值\(\overline{X}\),和(理想中)的总体均值\(\mu\),差了多远。
我们不知道总体的方差\(\sigma^{2}\),因此用样本方差\(S^{2}\)替代\(\sigma^{2}\),可得t统计量
\[t = \frac{\overline{X} - \mu}{\sqrt{\frac{S^{2}}{n}}}\]
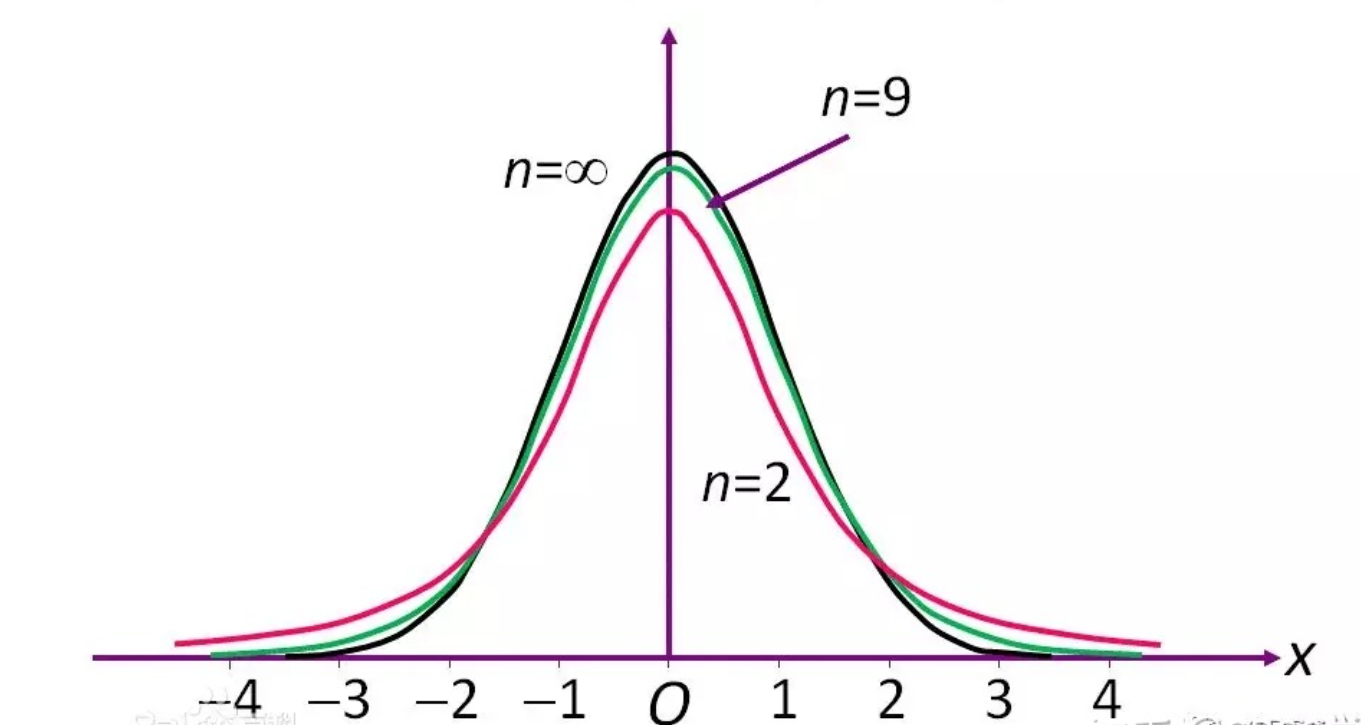
服从自由度为(n-1)的t分布。
t分布和自由度(样本数量)有关:
样本越少,t分布越平坦
样本越多,t分布越接近标准正态分布
19.7 单样本t检验
- t统计量服从自由度为(n-1)的t分布:(大样本时可以脑补成标准正态分布)
\[t = \frac{\overline{X} - \mu}{\sqrt{\frac{S^{2}}{n}}}\]
如果你的样本是从均值为\(\mathbf{\mu}\)的总体中抽样出来的,那么样本均值应该会服从上述分布。
如果t(绝对值)越大
如果总体均值为\(\mu\),那从中抽取的样本,其均值应该有比较大的概率也在\(\mu\)附近(t有比较大的概率在0附近)
从均值为\(\mu\)的总体中,抽到一批样本,其均值和\(\mu\)相差很远(t这么远),概率很小。
单样本t检验:
- 原假设:总体均值\(\mu\),和我们要检验的一个特定值\(\mu_{0}\),不存在显著差异
\[H_{0}:\ \mu = \mu_{0}\]
- 把\(\mu_{0}\)带入t统计量的表达式,可知我们手中样本的均值\(\overline{X}\)和\(\mu_{0}\)之间的关系
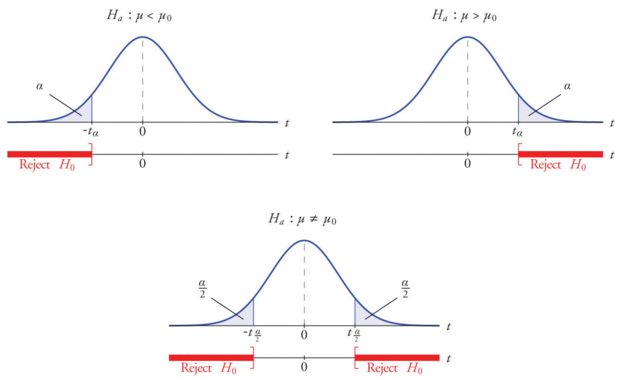
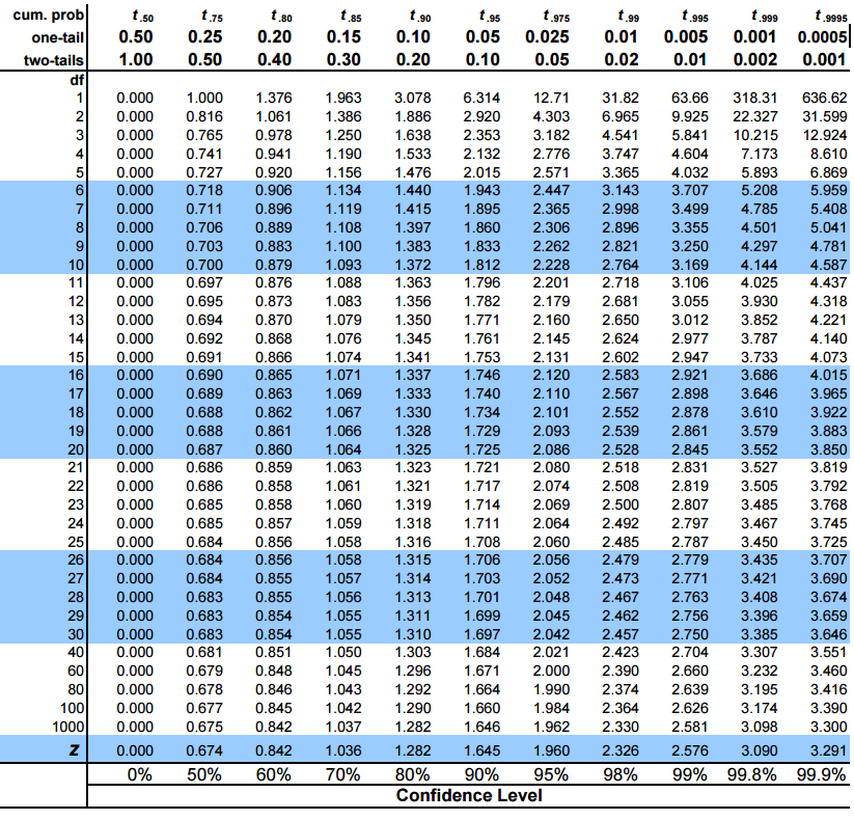
我们令显著性水平为\(\alpha\),习惯上\(\alpha\)可以取0.05或者0.01等。
\(\alpha\)实际上就是t分布(上图)中阴影(拒绝域)的面积。
指定一个\(\alpha\)(如0.05),我们可以反算出对应的t值(临界值)
如果从样本中算出的t值(的绝对值)比临界值(的绝对值)更大,那么t值就会落在阴影部分。
标准正态分布(或者样本很大的t分布),\(\alpha = 0.05\)(双侧,对应单侧0.025)对应的\(t = 1.96\),粗略算大概是2倍标准差
19.8 两独立样本t检验
很多研究,其实都可以归结为2个组别之间的比较,例:
新药的效果是否会优于老药?
一项政策有没有理想中的效果(和没有政策时相比)?
总体上,男生和女生的考试成绩,哪一方更高一点?
直观的做法是,进行抽样,然后比较两组样本的均值。
- 比较我们班男生和女生的平均考试成绩。
但是,因为抽样是随机的(回忆前文,班级成员的组成,一个人在这个学校的这个学院的这个班,而不在另一个班,基本上也可以认为是随机的),我们直接比较2组样本的平均分,中间还有一个疑问,均值有差异,但是否来自抽样的误差(随机因素)?
如果样本中女生平均90分,男生平均85分,我们可以说女生的成绩较佳吗?
这个平均分的差异,是否来自抽样误差?比如可能我们班”恰好”有几个厉害的女生,拔高了女生的平均分?
男女平均分,要差多少,我们才能认为这确实男女差异,而不是抽样误差?
19.8.1 零假设:均值间无差异
零假设:两组样本的均值无显著差异(如2组样本是从同一个总体中抽取的)
按照零假设,2组样本的均值之间差异,可以视为是抽样误差造成的偶然现象。
或,2个样本均值之间的差异,不代表他们在总体均值上有差异。
反过来:考虑你从同一个总体中抽2批样本,2批样本的均值也不可能完全相同。
零假设一般可以表示为:
\[H_{0}:\ \mu_{1} = \mu_{2}\]
其中\(\mu_{i}\)为两组样本所代表的总体均值。
如:零假设:男生和女生的平均成绩无差异。
19.8.2 备择假设(研究假设):均值间有差异
备择假设:两组样本的均值有显著差异。
2个均值之间的差异,大到一定程度,以至于不能被抽样误差所解释。
差异之大,难说是偶然。
备择假设一般可以表示为:
\[H_{1}:\mu_{1} \neq \mu_{2}\]
如:备择假设:男生和女生的平均成绩有差异。
19.8.3 均值间差异的抽样分布
如果你从同一个总体中抽取了2组样本,那么两组样本的均值的差异完全来自抽样误差。(对应:零假设:均值无显著差异)
你手里有2组样本,2组样本的均值相减,可以获得一个差值。
因为抽样是随机的,因此这个差值也是一个随机变量。
如果这2组样本来自同一个总体,均值之差(完全来自抽样误)会服从怎样的统计规律?
凭直觉,这2组样本的均值会很接近,因此均值之差应该围绕在0附近
从同一个总体中抽的2组样本,他们的均值有很大差异的概率应该很小
可以猜测,均值之差,可能服从类似正态分布的分布?
所以,均值的差,如果大到一定程度,我们就可以认为2组样本”几乎不可能”来自同一总体。
- 即:拒绝零假设:两组样本的均值有显著差异
如果2组样本分别服从正态分布,那么他们的均值的差,会服从\(N(\mu_{1} - \mu_{2},\sigma_{12}^{2})\)的正态分布。
其中\(\sigma_{12}^{2}\)是均值差的分布的方差(均值差也是一个随机变量)
这个值和自由度以及其他假设有关,统计学软件包如spss会帮你算
令样本均值差为 \(\left( {\overline{X}}_{1} - \ {\overline{X}}_{2} \right)\),其服从\(N\left( \mu_{1} - \mu_{2},\sigma_{12}^{2} \right)\),那么可得t统计量。
\[t = \frac{\left( {\overline{X}}_{1} - \ {\overline{X}}_{2} \right) - {(\mu}_{1} - \mu_{2})}{\sqrt{\sigma_{12}^{2}}}\]
- 在零假设下,如果2组样本来自同一个总体,那么\(\mu_{1} - \mu_{2} = 0\),
\[t = \frac{{\overline{X}}_{1} - \ {\overline{X}}_{2}}{\sqrt{\sigma_{12}^{2}}}\]
19.8.4 同方差和异方差
注意,我们仍不知道\(\sigma_{12}^{2}\)是多少
现在比较的是2组样本,因此两组样本的方差可能相同,也可能不同。
如果方差相同与否,使得\(\sigma_{12}^{2}\)的公式不同(略),且t统计量服从的不同自由度的t分布(略)。
SPSS中,我们通过莱文Levene的F方法,检验同方差性。
详情见后面的方差分析 ,这里暂略
具体见SPSS中的例子
19.8.5 显著性水平
如前文,我们用样本均值差的t统计量来描述2者差多远。
如果\({\overline{X}}_{1},\ {\overline{X}}_{2}\)的差异越大,\(\sqrt{\sigma_{12}^{2}}\)越小,则t(的绝对值)就越大。
t(的绝对值)大到什么程度,我们可以认为\({\overline{X}}_{1},\ {\overline{X}}_{2}\)的差异之大,不能用抽样误差来解释?
- 等于问:\(\left( {\overline{X}}_{1} - \ {\overline{X}}_{2} \right)\)落在t分布的那个区间?
我们令显著性水平为\(\alpha\),习惯上\(\alpha\)可以取0.05或者0.01等。
\(\alpha\)实际上就是t分布(上图)中阴影(拒绝域)的面积。
指定一个\(\alpha\)(如0.05),我们可以反算出对应的t值(临界值)
如果从样本中算出的t值(的绝对值)比临界值(的绝对值)更大,那么\(\left( {\overline{X}}_{1} - \ {\overline{X}}_{2} \right)\)的t值就会落在阴影部分
我们可以认为:如果\({\overline{X}}_{1},\ {\overline{X}}_{2}\)真的是从同一个样本中抽出来的,那么他们之间差异如此之大,其概率低于\(\alpha\)(如0.05)
若离0足够远,\({\overline{X}}_{1},\ {\overline{X}}_{2}\)的差异足够大,使得拒绝(他们无差异的)原假设。
标准正态分布(或者样本很大的t分布),\(\alpha = 0.05\)(双侧,对应单侧0.025)对应的\(t = 1.96\),粗略算大概是2倍标准差
19.9 配对样本(同一组样本前后比较)
前面研究的是:对2组独立抽取的样本进行比较,检验他们的均值是否有显著的差异(是否来自同一个总体)。
现在的问题是:同一批样本,但在2个不同时间的观测值,是否有差异
同一个人,在不同的时间上自己和自己比较。
注意:在不同的时间上,独立地对同一个总体进行2次抽样,要应用独立抽样的情况。
原假设:同一批样本的两次观测数据,其均值无差异。
做法:
把前后样本,两两相减,得到差值样本。
检验差值样本的均值是否和0有显著差异。
选择显著性水平,观察t值和P值。
19.10 方差分析
前面讲的是对比2个组。但我们想研究多个组,应该如何?
比如,我们考虑,考试评级不同(A、B、C等的)同学,毕业工资有没有不同。考虑A单位的药物,B单位药物,C单位药物疾病的影响,等等。(注:这里说的是“一个变量有多于2个取值”,即单因素/单变量方差分析)
理论上,我们可以每2个组之间做t检验:A和B,B和C,C和D,因此可以得到3个t值,但是这样做的问题:
- 分组增加,要做的t检验会非常多。
- 有时候很难解释。
我们想知道,n组样本之间是否存在差异
或“n组样本是否来自同一个总体”,做一次性的判断。
19.10.1 方差分析的逻辑
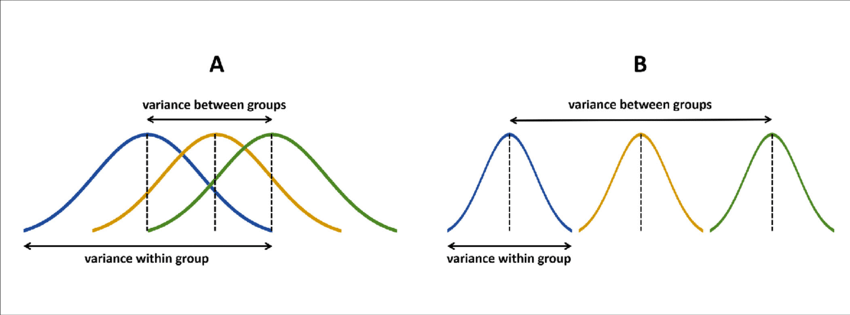
零假设:组之间没有差异
备择假设:最少有2个组之间存在差异
组内方差:原始数据,对于组内均值的偏离
组间方差:各组的均值之间的距离或者偏差
F值(后面有公式):分子表示组间方差,分母表示组内方差,因此F值是组间差异和组内差异的比值。F值越大(更接近于下图B),则组间方差相对组内方差越大,组间存在差异的可能性也越大。
19.10.2 平方和
为了把F值算出来,首先需要计算3个平方和:总体平方和SST,组间平方和SSA,组内平方和SSE。
总体平方和,等于每个样本和总体均值之差的平方和。
\[SST = \sum\left( X_{i} - \overline{X} \right)^{2}\]
组内平方和,每个样本,和各自的分组的均值之差的平方和
\[SSE = \sum\left( X_{i} - {\overline{X}}_{g} \right)^{2}\]
组间平方和,每个分组的均值,和总体均值的差的平方,乘以每个组的元素个数,再求和
\[SSA = \sum N_{g}\ \left( {\overline{X}}_{g} - \overline{X} \right)^{2}\]
19.10.3 均方(方差)
平方和会随着样本变大而变大,比如从同一个总体中抽取200个样本,其平方和比抽取20个样本的平方和更大。
我们要排除样本数量的影响,把不同组放在同一个标准下比较。
把组内平方和和组间平方和,除以各自的自由度:
组间均方 = 组间平方和,除以组间自由度
\[MSA = \frac{SSA}{df_{a}}\]
\[df_{a} = k - 1\]
其中k为组数
同理,组内均方 = 组内平方和,除以组内自由度
\[MSE = \frac{SSE}{df_{e}}\]
\[df_{e} = N_{t} - k\]
其中\(N_{t}\)是样本总数。
19.10.4 F值
终于到了F值:组间均方,对组内均方的比值。
\[F = \frac{MSA}{MSE}\]
易见:如果组之间确实有差异,那么组和组之间的距离可能比较远,组间均方就会比较大,F值的分子就会比较大。因此,F值越大,多个组之间有差异的可能性也越大。
反之:如果F值很小,不同组的数据几乎重合在一起,就不能排除不同组的数据无显著差异,或者说来自同一个总体。
显著性水平等概念,和t检验类似。
19.10.5 其他
F值一般用于三个或更多样本均值的比较。
一般用于分析连续变量。
多个分组应服从正态分布
19.11 非参数检验:卡方检验
问题:现有的数据,是否服从某个特定的分布?进行一次性的回答。
如:老师点名是否服从每周一次均匀分布(老师是否每周点名一次)?等等
19.11.1 卡方检验:
原假设:样本来自的总体分布,和期望分布/某个理论分布,无显著差异。
卡方统计量:
\[\chi^{2} = \sum_{i = 1}^{k}\frac{\left( f_{i}^{0} - f_{i}^{e} \right)^{2}}{f_{i}^{0}}\]
假定一个学期16周,问老师点名是否符合”每周点一次”的均匀分布?
其中:
\(k\)是分组数:16周
\(f_{i}^{e}\)期望频数:
每周点一次
,就是每周点名的期望次数是1(每个组内的观测数是1)\(f_{i}^{0}\)观测频数:每周真实的点名次数。
例:老师一个学期只点名了2次,开学和期末复习课。
第1和16周\(f_{1}^{0} = f_{16}^{0} = 1\)
其他j不等于1和16:\(f_{j}^{0} = 0\)
1, 0, 0, …. 1
预期分布:每周点名
第i周\(f_{i}^{e} = 1\)
1,1, … 1
直观上,卡方所表述的,只是观测的情况(每组的样本数)和期望情况,到底有多大差异。
如果你获得了一个很大的\(\chi^{2}\),或者很小的p值,即可以拒绝原假设:现实和理想差异太大,以至于可以拒绝现实分布服从理想分布的原假设。
19.11.2 K-S检验
同样,K-S检验也考察样本是否符合某个分布。卡方考察分类数据(落入每个类别的观测数,和预期值有多少差异),K-S适合考察连续变量:
原理:计算理论的累计分布\(F(x_{i})\),计算实际样本中的累计分布\(S(x_{i})\),然后对比两者的最大差异有多大\(D\left( x_{i} \right)\)
\[D = \max{\lbrack|S\left( x_{i} \right) - F\left( x_{i} \right)|\rbrack}\]
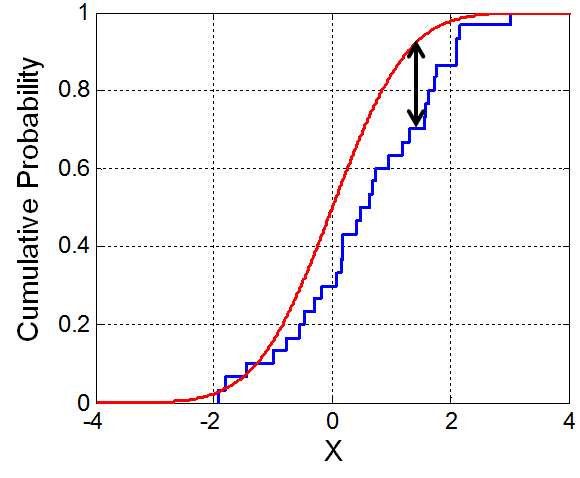
直观理解:理论分布的累计分布函数是红线,样本的累计分布是蓝线。那么D值反映的,就是理论分布和样本分布之间的最大的差异有多大。
D越大(P越小),样本和理论的差异就越大:和t检验以及F检验类似。
19.11.3 游程runs
问:一个样本,是否随机。要求:01序列,或者可以转为01。
游程:连续出现相同观测值的次数(或者:把相邻的相同变量合并)。比如一个序列
1 1 0 0 1 1 0 0 1 0,游程=6
1 1 1 1 0 0 1 1 0 1 ,游程=5
原理:如果一个序列是随机的,那么连续1、连续0,或者01交替的概率,都不会太高或者太低。
111111111111:1
00000000000:1
01010101010:n
计算一个Z统计量(公式略),近似服从正态分布。
19.12 两独立样本非参数检验
前面的检验考察的是一组样本是否服从某个分布。这里考察的是,2组样本是否来自同一个总体(具有相同的分布):分布的形状,和正态分布差异很大。
19.12.1 两独立样本曼-惠特尼U检验
原理:把2组样本混合,升序排序,然后看2组样本的平均秩(样本的排名)。
直观理解:如果2组样本来自同一个总体,混合之后,2组样本混合后的元素的排名的均值应该很接近。
12121122211221212121:比较充分混合,平均秩(平均排名)比较接近
11111111111222222222:1组和2组的平均秩(平均排名)差异很大
22222222221111111111:
计算公式略。
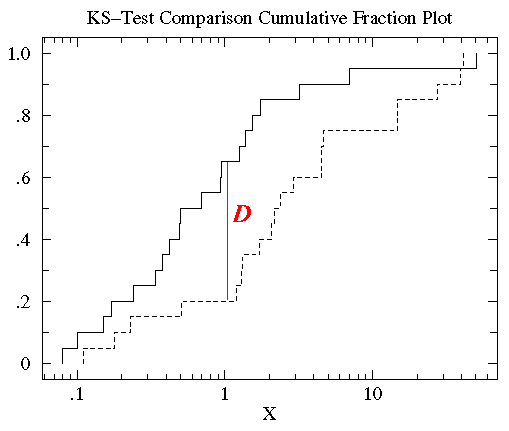
19.12.2 两独立样本K-S检验
和单样本K-S类似,检验2组样本的累计分布的D统计量。但是使用的是变量的秩(排序)
原理:把2组样本混合,升序排列。计算2组样本的秩的累计频率和频数。再计算累计频率的差的绝对值,计算D统计量。
同理:直观理解,D越大,则2组样本差异越大,有可能拒绝原假设。
19.12.3 两独立样本W-W游程检验
原理:2组样本,混合,升序排序,然后按照分组来标记。如12112221122121212,1表示来自第一组,2表示来自第二组。计算游程。
直观理解:如果两组差异很大,排序之后可能变成1111122222,那么游程就会较小。如果两组差异很小,排序后可能会相间出现,如21122121,那么游程就会较大。
19.12.4 两独立样本极端反应
原理:2组样本,混合,升序排序。计算其中一组样本(控制样本)的最大秩和最小秩。
定义跨度\(S = Q_{\max} - Q_{\min} + 1\),直观理解。如果2组样本差异很小,可以充分混合,那么跨度就会较大。反之,如果差异较大,那么其中一组可能聚集在序列的一侧,跨度会较小。
12112221122121212
注:为了避免极端值的影响,可以先进行5%剔除极端值(截尾)
19.13 多独立样本的非参数检验
考虑了单样本,两样本,现在可以考虑多样本。
类似地,多样本的原假设也是”多个样本之间的(某个统计量)无显著差异”。
19.13.1 多独立样本中位数检验
多独立样本中位数检验的原理:如果多组样本的中位数没有显著差异,或者说多组样本都有共同的中位数,那么混合样本后的中位数,应该也应该接近于每个分组的中位数。
打个比方:把混合样本排序后,从正中间一刀切开,这一刀也应该刚好切在每个分组的正中间。
例如:考虑4个城市的儿童身高进行中位数检验,计算每一个城市高于和低于共同中位数的儿童数量:
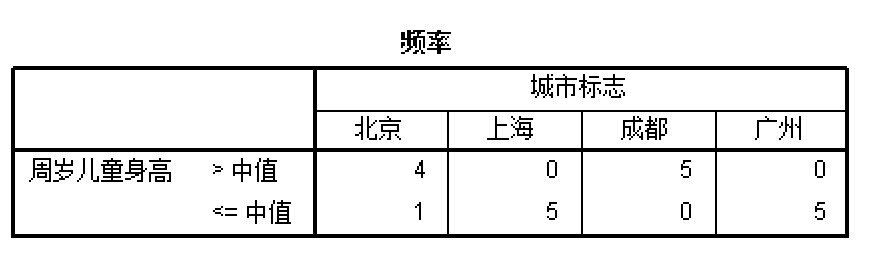
每个城市都是5个样本,可以想象,如果4个城市的儿童身高具有相同的中位数,那么每个城市大于和小于中位数的期望(上表中的每一个数字)值都应该是\(f_{i}^{e} = 2.5\),把观测值代入,即可算出卡方值。
\[\chi^{2} = \sum_{i = 1}^{k}\frac{\left( f_{i}^{0} - f_{i}^{e} \right)^{2}}{f_{i}^{0}}\]
(具体见例子)
19.13.2 多独立样本K-W检验
原理:曼-惠特尼U检验的多样本推广。
曼-惠特尼U检验的原理:2组样本混合,排序,计算2组样本的平均秩(排名),如果样本来自同一个总体,那么2组样本应该充分混合,两组样本的元素排名的均值应该很接近。
K-W检验的原理:多样本混合,排序,同样计算来自不同组的平均秩,比较多个平均秩的差异。
比较多组样本的均值是否相同:方差分析的原理(这里是比较多组样本的秩的均值是否相同)
构造K-W统计量:(看起来几乎就是方差分析的公式)
\[KW = \frac{秩的组间离差平方和}{秩的总离差平方和的平均}\]
具体公式略。
19.13.3 多独立样本J-T检验
原理略。
19.14 两配对样本
19.14.1 两配对样本McNemar检验
用于两分类数据的前后比较,如好坏、正反等等,在实验前后是否有变化。
- 首先,对同一批被试(人或者动物等),问一个只有两个答案的问题(或者做一个2种结果的测试,高低,快慢等等),
比如:你觉得你考试能过80分以上吗?分别记录选择两者的人数。
- 对被试进行一个处理(实验)
比如:复习1天。
再问同样的问题。你觉得你考试能拿80分以上吗?分别记录选择两者的人数。
考察:处理前后,
对同一个问题转变回答的人数
。回答无变化的人不管。
比如:可以 -> 不可以,不可以 -> 可以,分别的人数。
如果状态转换的人数量相当,那么这个处理(复习1天)对总体的分布就没造成什么影响。
比较2类人的人数是否相等?等价于做一个概率为0.5的二项分布检验!
| 复习后 | |||
|---|---|---|---|
| 不能过 | 能过 | ||
| 复习前 | 不能过 | 3 | 4 |
| 能过 | 2 | 3 |
学习前后都认为不能过 :3人
学习前后都认为能过 :3人
学习前认为能过 ,学习后认为不能过 :2人
学习前认为不能过 ,学习后认为能过 :4人
McNemar检验:
检验的是状态转变的频数:上例中的3、4。
如果2种状态转换的人数相当,那么可以认为这个处理,对总体分布没有产生什么影响。
其实等于问:4个格子中,两种状态转换的频数,是不是相当?即:可以做一个概率为0.5的二项分布检验。
19.14.2 两配对样本的符号检验
实验后的数据,减去实验前的数据,保留正负号。
----+++++---++++------+++-++-----
如果实验没有对被试产生显著的影响,那么正负号的数量应该相当。
可以对正负号的数量做概率为0.5的二项分布检验。
例如:研究喝奶茶对体重的影响。
- 找一批被试,测量体重。
- 让他们喝1个月奶茶。
- 测量同一批被试的体重。
- 前后体重相减,保留正负号。可能得到一堆加号:
+++++++++++++++++++++++++++++
显然和概率为0.5的二项分布差异极大。
19.14.3 两配对样本的符号秩检验
实验后的数据,减去实验前的数据,保留正负号和差额的绝对值。
按差额绝对值排序,把数据分为正号组和负号组,计算2个组的平均秩。
直觉:如果实验前后,样本没什么变化,那么可以预见变大和变小的样本,应该相互参杂在一起,正号组和负号组的平均秩应该相当。
19.15 多配对样本的非参数检验
19.15.1 多配对样本的Friedman(傅莱德曼)检验
基本原理:
你有N个被试,每个被试要做多种处理,可以对处理的结果进行排序。你要比较这几种处理整体上有没有差异。
如:你有10种商品(被试),3种促销方式(3种treatment),对比多种促销方式,10种商品的销量有没有差异。
3种促销方式下,促销的商品都是那10种,这个多配对样本的检验。
对照:复习前的考试成绩,复习后的考试成绩,考试的同学还是那几个:2配对样本。
商品1, 有3种促销方式:效果可以排序,得到秩(1,2,3的顺序)
商品2, 有3种促销方式:效果可以排序,得到秩(1,2,3的顺序)
| 商品编号 | 促销方式1 | 促销方式2 | 促销方式3 | 形式1的秩 | 形式2的秩 | 形式3的秩 |
|---|---|---|---|---|---|---|
| 1 | 128 | 172 | 99 | 2 | 3 | 1 |
| 2 | 46 | 58 | 52 | 1 | 3 | 2 |
| 3 | 104 | 144 | 100 | 2 | 3 | 1 |
| … | ||||||
| 平均秩 | 2.1 | 2.5 | 1.4 |
基本思想:
如果3种treatment(本例为促销形式)是无差异的,那么形式1 、形式2和形式3的平均秩,应该非常接近(更直觉的是,你把同一种促销方式重复三遍,那123的次序就完全是随机的了)。
如果形式1的效果最好,那么可以预见,形式1的平均秩应该最大。反之则最小。
Friedman统计的计算公式略
原假设是:无差异。因此,如果遇到很小的p值时,可以拒绝原假设,认为三者有差异。
19.15.2 多配对样本的Cochran(柯克兰)Q检验
同样是同一批被试的多个处理(上例种是10种商品的3种促销方式),但这里答案是二值变量(01变量),如”好/坏”,及格/不及格
。
例如,15个乘客,对3家航空公司打分(1好/0不好)
(本质上,你有一个15行的表格,三列01数据,问这三列01数据,整体有没有差异。)
| 乘客号 | 甲航空公司 | 乙航空公司 | 丙航空公司 | Li |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 2 |
| 2 | 1 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 | 1 |
| … | ||||
| 15 | 0 | 1 | 0 | 1 |
基本思想:
假如3者没有区别(比如,15名乘客,把甲航空公司重复测试了3次)。那么从列来看,这3列出现1的比例(概率)应该是相同的。或者说,15名乘客,认可这3家航空公司的比例应该一样。
如果甲航空公司最好,那么1的比例应该最高;反之最低。
上述这个概率,也和每个乘客的评价标准有关。严格的乘客,1较少0较多;反之1较多0较少。
柯克兰Q统计量的表达式略。
原假设:多组的1概率无差异。因此,如果遇到很小的p值时,可以拒绝原假设,认为三者有差异。
19.15.3 多配对样本的Kendall(肯德尔)W协同系数检验
要回答的问题是:评价者的评价标准是否一致,或不同组的平均秩有没要显著差异。
原假设:评价标准不一致(组间的平均秩无差异)。(注:这个原假设是”标准不一致=组间的平均秩无差异”)
4位评委给6位歌手打分。(4个被试,6个treatment;6个人吃4种药)
利用傅莱德曼检验,看6个歌手的分数是否有差异。如果无显著差异,那么可以认为评委打分是随意的,或者分歧极大(有人给高分和有人给低分),或不具一致性。(每个歌手 = 每个treatment)
如果评委打分具有一致性,那么厉害的歌手,应该较多评委给高分;反之较少。那么平均秩的应该有显著差异,好歌手的平均秩应该较大,反之较小。
进一步计算W协同系数(公式略),W如果接近1,则组间秩的差异越大。0则越小。
| 评委 | 1号歌手的秩 | 2号歌手的秩 | 3号歌手的秩 | … | … |
|---|---|---|---|---|---|
| 1 | 1 | 4 | 2 | … | … |
| 2 | 1 | 4 | 2 | … | |
| 3 | 1 | 5.5 | 2 | … | |
| … | |||||
| 平均秩 | 1 | 4.38 | 2 | … |
19.16 相关
19.16.1 相关系数
相关系数r在[-1,1]之间
r > 0 表示正的线性相关,反之表示负相关;
r= 0表示不存在线性关系。r =1表示完全正相关,-1表示完全负相关。
但一般我们不能直接用相关系数来判断相关关系:
因为抽样是随机的:两个变量高度相关,但你手中的样本可能不相关(比如样本太少看不出来)。两个变量不相关,但你手里的样本恰好相关(偶然因素)。
因此,还需要做统计检验。
原假设:都是0相关(不相关)
19.16.2 皮尔逊Pearson简单相关系数
公式:
\[r = \frac{\sum_{i = 1}^{n}\mspace{2mu}\left( X_{i} - \overline{X} \right)\left( Y_{i} - \overline{Y} \right)}{\sqrt{\sum_{i = 1}^{n}\mspace{2mu}\left( X_{i} - \overline{X} \right)^{2}}\sqrt{\sum_{i = 1}^{n}\mspace{2mu}\left( Y_{i} - \overline{Y} \right)^{2}}}\]
简单相关系数是对称的:x和y的相关系数,等于y和x的相关系数
相关系数是无量纲的
相关系数研究的是线性关系
要判断相关的显著性,需要做一个t检验,t统计量为
\[t = \frac{r\sqrt{n - 2}}{\sqrt{1 - r^{2}}}\]
服从自由度为n-2的t分布。
先把相关系数r值计算出来,在通过r和自由度n-2计算t值,再查表。其他就和前面的t检验完全一致。
19.16.3 斯皮尔曼Spearman等级相关系数
用于处理”定序变量”:如优、良、中、及格、不及格等。
整个原理和皮尔逊简单相关系数一致,但因为定序变量本身只有顺序的意义,一般无法直接进行加减等计算。因此先转化秩,再计算皮尔逊相关系数。
例如:以排名(秩)来考虑每一个同学考试分数。(本身是定序变量,或者由连续变量转为定序变量)
如果两个变量完全正相关,变量的秩完全同步,r趋向于1。
复习时间第一长的同学,考试第一高分;复习时间第二长的同学,考试第二高分。… 复习时间最短的同学,考试最低分。
如果两个变量完全负相关,变量的秩正好相反,r趋于-1。
上课走神时间最短的同学,考试最高分;上课走神时间第二短的同学,考试第二高分;
r 在-1到1中间,则同步性中等。r=0则完全不同步,几乎可以看出随机。
小样本时,r服从斯皮尔曼分布;
大样本时,计算Z统计量,近似服从正态分布;
\[Z = r\sqrt{n - 1}\]
SPSS会自动帮你计算。
19.16.4 肯德尔Kendall \(\mathbf{\tau}\)相关系数
定序变量,非参数检验
大体原理
我们有A到H共8个人,每个样本2个两个数据,身高和体重。按其中一个变量的秩排列,以身高为例。
| 人 | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| 身高的秩 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 体重的秩 | 3 | 4 | 1 | 2 | 5 | 7 | 8 | 6 |
A身高最高,体重第3,记为(1,3)
身高和体重同时小于A的(括号中2个数都比A大的)
有B(2,4),E(5,5),F(6,7),G(7,8),H(8,8)
那么”一致对(同序对)“,就有AB,AE,AF,AG,AH。A贡献的一致对有5个。
同理,B、C、D、E、F、G、H分别贡献4、5、4、3、1、0、0个。
那么一致对的数量\(U = 5 + 4 + 5 + \ldots = 22\)
总对数是28,非一致对的数量是\(V = 28 - 22 = 6\)
计算\(\tau\)统计量
\[\tau = (U - V)\frac{2}{n(n - 1)} = \left( \frac{22 - 6}{28} \right) = 0.57\ \]
小样本下\(\tau\)服从Kendall分布
大样本下计算Z统计量
\[Z = \sqrt{\frac{9n(n - 1)}{2(2n + 5)}}\]
近似服从正态分布。
SPSS会自动帮你计算。
19.17 偏相关分析
例如:有一个研究人员发现,身高和薪水之间有显著的正相关关系。但事实是否真的如此?
实际上这个判断可能忽视了一些重要的因素,如”性别”。其他研究发现:
男性的平均身高高于女性;
男性的平均工资也高于女性(可能来自职业选择或者职场歧视等等)
因此,原来的观察:身高越高,薪水越高
,可能很大程度上源于性别的差异。
那么问题就是:身高本身到底是否影响薪水?
偏相关系数:控制了(排除了)其他变量的影响后,两个变量的相关系数。
我们有3个变量,y,x1,x2
我们考虑的是x1和y之间相关性,但要排除x2的影响。
那么x1和y的一阶偏相关系数为:
\[r_{y1,2} = \frac{r_{y1} - r_{y2}r_{12}}{\sqrt{(1 - r_{y2}^{2})(1 - r_{12}^{2})}}\]
其中
\(r_{y1}\)为y和x1的相关系数
\(r_{y2}\)为y和x2的相关系数
\(r_{12}\)为x1和x2的相关系数
同样,我们不能只用相关系数来考察相关关系,还是要做假设检验。
原假设:线性偏相关系数为0(无偏相关关系)
计算t统计量
\[t = r\sqrt{\frac{n - q - 2}{1 - r^{2}}}\]
服从n-q-2个自由度的t检验。其他同前述的t检验。
19.18 回归
注:统计学(SPSS)的回归和计量经济学中的回归,技术手段是一样的,但思考方式不同。
计量经济学中的回归:
只要不产生多重共线性,应该把影响回归的因素(变量)全部作为控制变量加入;
对于会影响回归的因素,但无法找到对应的数据,这就产生遗漏变量的问题,可以考虑采用代理变量、面板数据回归等等方法。
加入控制变量,考虑的是”逻辑上”该因素是否会影响你的回归,而不论在在多元回归中这个因素的显著性如何:逻辑上有影响的因素,即使在回归中不显著也应该加入和保留。
存在内生性(包括上述的遗漏变量、自我选择等等问题),可以考虑采用工具变量、断点回归、DID等识别方法。
19.18.1 为什么要做回归
回归要回答的问题:因素x(自变量、因子、解释变量),是否会、会如何影响因素y(因变量、被解释变量)。
注意到:前面学的方差分析,其实也是回答这个的问题!
方差分析问:几个分组之间有没有显著差异。
例:
问:几种不同促销方式下,商品的销量有没有显著差异?
= 不同促销方式的分组,商品销量的均值有没有显著差异?
= 不同促销方式是否会影响商品的销量?如何影响?
= 促销方式 = 因素x,商品销量 = 因素y:因素x是否或如何影响因素y?
但是:方差分析所研究的问题是”不同分组下的均值的差异” = 分类变量影响连续变量
:
不同促销方式:分类变量
商品的销量:连续变量
回归要回答的问题是”连续变量(或者分类变量)影响连续变量(或者分类变量)”:粗糙地理解,回归分析涵盖了方差分析,但如果自变量是分类变量,其回归对影响的解释往往没方差分析那么直观。
所以:如果你被解释变量y是连续变量,x是连续变量,那么可以选择回归分析;如果x分类变量,那么可以选择方差分析或者回归分析。但如果很明白你要做什么,那么直接选择回归也可以。
19.18.2 一元回归
x影响y = x的变化会引起y的变化:
数据中的x和y都要有变化(或者说散点图散布比较宽),我们才能从数据中识别x和y的关系。
例:考虑复习时间x和考试成绩y之间的关系。如果考试过于简单,所有同学都拿100分,那么即使复习时间和考试成绩有关系,我们也无法从这个数据中研究发现。
一元线性回归模型:
\[y = \beta_{0} + \beta_{1}x + u\]
x:自变量
y:因变量
\(u\):误差项、干扰项:除了x之外,还影响y的因素
例如:工资wage可能和学历edu有关
\[wage = \ \ \beta_{0} + \beta_{1}edu + u\]
那么这个模型中的误差项\(u\),就包括了除了学历edu之外的所有影响工资的因素,如个人的智力、工作经验等等其他因素。
注意:很多会影响y的因素,可能因为种种原因没有进入你的模型(典型的原因是数据中没有),如工作经验,这些因素对工资的影响都在\(u\)中。计量经济学和统计学的习惯稍有不同,计量经济学一般称之为”误差项”或者”干扰项”,但一般不称为”随机因素”。
假定误差项的均值为0:
\[E(u) = 0\]
只要回归方程中存在截距项\(\beta_{0}\),那么我们总是可以让\(E(u) = 0\)
\(u\)的平均值和x无关
\[E\left( u \middle| x \right) = E(u)\]
上述两个假设,成为零条件均值假设
\[E\left( u \middle| x \right) = 0\]
19.18.3 普通最小二乘法的解释
一元回归
我们有的数据:对于每个样本,我们有x和y
例:
对于每个人,有其学历x和工资y
对于每个人,有其复习时间x和考试成绩y
我们要想做的事:我们希望判断,x和y之间有没有关系,有什么关系(特指因果关系)
例:
学历x影响工资y吗?如何影响?
复习时间x影响考试成绩y吗?如何影响?
我们要建立的模型:我们假定x和y之间有线性关系(对线性关系解释不展开):
\[y_{i} = \beta_{0} + \beta_{1}x_{i} + u_{i}\]
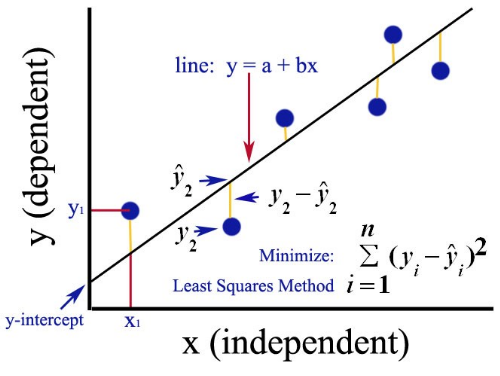
我们知道 \({\widehat{y}}_{i} = \beta_{0} + \beta_{1}x_{i}\)是一条直线(\(y = ax + b\)都是直线,小学数学),对于每个\(x_{i}\)(这是我们观测到的值),对应一个回归线上的点 \({\widehat{y}}_{i}\);或者说, \({\widehat{y}}_{i}\)都落在回归线上。
散点是我们的数据,回归线是我们的模型:
我们试图用一条线,来代表两个变量之间线性关系。
所以我们的问题就变成了:如何找到一条最好的线(最好的标准是什么?),最能代表2个变量之间的关系?
在回归模型 \({\widehat{y}}_{i} = \beta_{0} + \beta_{1}x_{i}\)中,就是找到最好的\(\beta_{0}\)和\(\beta_{1}\)的估计值(同样,我们没有总体的数据,只有样本的数据),对应直线的截距和斜率。
OLS:普通最小二乘法
对于同样的\(x_{i}\),观测值\(\left( x_{i},y_{i} \right)\),和回归线直线的点\(\left( x_{i},{\widehat{y}}_{i} \right)\),2个点之间的垂直距离\({\widehat{y}}_{i} - y_{i}\),称为残差\(u_{i}\)。(符号也可以用\(\varepsilon_{i}\),用u好输入一点)。
OLS的”最好”的标准:如果有\(\beta_{0}\)和\(\beta_{1}\),使得残差平方和最小,那这个估计值 \({\widehat{\beta}}_{0}\)和\({\widehat{\beta}}_{1}\)是对总体回归线的最好的估计。
\[\sum_{i = 1}^{n}\left( y_{i} - {\widehat{y}}_{i} \right)^{2} = \sum_{i = 1}^{n}\left( u_{i} \right)^{2}\]
图中:找到一条直线,使得所有的黄色垂直线的平方的和最小。
回归系数的数学表达式略。
就找到了我们对\(\beta_{0}\)和\(\beta_{1}\)的估计值 \({\widehat{\beta}}_{0}\)和\({\widehat{\beta}}_{1}\),所以我们的模型、我们估计的x和y之间的关系、我们估计出来的直线,可以表示为
\[{\widehat{y}}_{i} = \ {\widehat{\beta}}_{0} + {\widehat{\beta}}_{1}x_{i}\]
注意:系数\({\widehat{\beta}}_{1}\)(回归线的斜率),正是我们关心的因果关系。
例子:工资 vs 学历
\[{\widehat{工资}}_{i} = \ {\widehat{\beta}}_{0} + {\widehat{\beta}}_{1}学历_{i}\]
\({\widehat{\beta}}_{1}\)表示学历每提高一单位(具体是多少,要看你的数据),工资平均来说能提高多少。(x横向移动一单位,回归直线提高多少单位)
例子:复习时间 vs 考试成绩
\[{考试成绩}_{i} = \ {\widehat{\beta}}_{0} + {\widehat{\beta}}_{1}复习时间_{i}\]
\({\widehat{\beta}}_{1}\)表示复习时间提高一单位(具体是多少,要看你的数据),考试成绩平均来说能提高多少。
注:如果你关心的是因果关系(正如一般的经济学家那样),那么你最关心的就是斜率,而不是其他。
如果不能拒绝\({\widehat{\beta}}_{i} = 0\),我们就不能拒绝x和y没关系的假设。最起码,不论x和y有没有关系,以现有的模型和数据,看不出来。(考虑一个统计量是否异于0:t检验!)
多元回归
同理,多元回归的情况也类似,不过回归线,从直线变成了超平面。
\[{\widehat{y}}_{i} = \ {\widehat{\beta}}_{0} + {\widehat{\beta}}_{1}x_{i1} + {\widehat{\beta}}_{2}x_{i2}\ldots\ \]
回归系数有着相同的解释,但多一个定语:在其他条件保持不变的情况下。
在其他条件保持不变的情况下,自变量提高1单位,因变量提高多少。
例:考虑学历和工作经验对工资的影响:
\[{\widehat{工资}}_{i} = \ {\widehat{\beta}}_{0} + {\widehat{\beta}}_{1}学历_{i} + {\widehat{\beta}}_{2}经验_{i}\]
\({\widehat{\beta}}_{1}\)的解释就变成了:工作经验保持不变的情况下,平均来说,学历对工资的影响。
\({\widehat{\beta}}_{2}\)的解释就变成了:学历保持不变的情况下,平均来说,工作经验对工资的影响。
反过来理解:
一个人的工资,是无数种因素作用的共同结果、相互影响,我们怎么才能把感兴趣的因果关系(比如你要做的研究是学历 vs 工资),从无数中关系中提取出来?
你要做的,是把影响工资的因素,尽可能多地作为控制变量加入模型中(在满足一定的条件下,例如避免完全共线性)。
我们称之为”控制了某个因素”:例如”控制了工作经验之后,学历对工资的影响系数是\({\widehat{\beta}}_{1}\)“:
使用夸张的比喻:当你把世界上所有影响工资的因素,全部加入模型,那么你计算的\({\widehat{\beta}}_{1}\),排除世界上一切影响工资的其他因素,将会是一个世界上最准确的,学历对工资的影响的估计。
但现实一定做不到这一点:必然有些影响工资(又和学历有关的因素),我们无法获得;如果这个因素还比较重要,我们就产生了”遗漏变量”的问题。
例如:一个人的智力(还有健康、工作行业、心情好不好等等)会影响工资,又和学历有关,如果遗漏了智力,我们就不能说”在其他所有重要因素保持不变的情况下,学历对工资有什么影响”。有一些因素没有排除干净,使得我们对”学历对工资的影响”里面,混合了其他重要的东西,比如智力。
因为智力高,可能学历也比较高,同时工资也比较高:三者正相关。
如果我们没有智力的数据,就无法把智力加入模型,也就无法排除这个因素的影响。因此,这个模型中,学历对工资的影响(你所估计的系数的大小),可能有一部分是由智力造成的(实际上,你估计的系数可能高估了学历对工资真正的影响:提高1单位学历的工资的增幅,其中有一部分是高学历者可能具备的高智力提高所贡献的)。这就是所谓估计的”偏误”。
原则上,要估计得准确,你不希望遗漏这些重要的变量(遗漏变量是所谓”内生性”问题的来源,这里不再展开)。因此控制变量能添加尽量添加;如果数据中没有,计量经济学家发明了很多方法,如代理变量、工具变量、断点回归、DID等,不再展开。
自选择问题
看医生能提高健康水平吗?
直观理解:去医院的次数越多,可能健康状态越差:因为健康状态差的人,会去更多的医院。
\[健康_{i} = \beta_{0} + \beta_{1}看医生_{i} + u_{i}\]
我们可能看到\(\mathbf{\beta}_{\mathbf{1}}\)是负数:看医生会提高健康状态(\(\beta_{1}\)本质上是正数),但是因为病人存在自选择(健康状态差的人,会去更多的医院
),因此我们从回归中可能看到相反的结果!
同样的问题:增加警察数量能提高地区的治安水平吗?
遗漏变量和自选择本质上是同一个问题:
遗漏的变量:病人原来的健康状态。如果我们控制了病人原来的健康状态,就排除了”健康状态差的人,会去更多的医院”这个自选择问题:\(\beta_{1}\)=在保持原来健康状态相同的情况下,看医生对健康的影响(近似理解:同样健康状态的人内部相互比较)
\[健康_{i} = \beta_{0} + \beta_{1}看医生_{i} + \beta_{2}原健康状态 + u_{i}\]
(简单回归操作)
- 如何求系数的估计(求\(\beta\)的值),其公式在这里略去,一般计量教科书都有。
- 系数估计之外最重要的问题是假设检验,
回归是否显著
指的就是假设检验。
假设检验要回答的问题是:
你在模型中估计的系数\(\beta\)有多准确?毕竟你拥有的只是一批样本,是总体的一个很小的子集,那么你从这个样本中估计的\(beta\)能代表真实的情况吗?
换句话说,你有多大的把握,你估计的\(\beta\)的真实值不是0?(某些情形下比较的是1)
下面会过一遍假设检验的大致原理。
19.18.4 离差平方和
一堆术语,但不同教材或软件采用的缩写可能不太一样(虽然含义并无不同)。
回归平方和/解释平方和:
SSR(Sum of Squares for Regression) = ESS (Explained Sum of Squares)
度量的是相对于样本的均值,回归线上的点的散步程度。
\[SSR = \sum_{i = 1}^{n}\left( {\widehat{y}}_{i} - \overline{y} \right)^{2}\]
残差平方和/剩余平方和:
SSE(Sum of Squares for Error)= RSS (Residual Sum of Squares) = SSR(Sum of Squared Residuals)
\[SSE = \sum_{i = 1}^{n}\left( y_{i} - {\widehat{y}}_{i} \right)^{2} = \sum_{i = 1}^{n}\left( u_{i} \right)^{2}\]
度量的是样本点和回归线的差,即上面说的残差。
总离差平方和:
SST(Sum of Squares for Total) = TSS(Total Sum of Squares)
度量的是样本点相对自己的均值的散布程度。
三者的关系是:
SST = SSR + SSE (SPSS采用的缩写)
\[SST = \sum_{i = 1}^{n}\left( y_{i} - \overline{y} \right)^{2} = \sum_{i = 1}^{n}\left( {\widehat{y}}_{i} - \overline{y} \right)^{2} + \sum_{i = 1}^{n}\left( y_{i} - {\widehat{y}}_{i} \right)^{2}\]
总离差平方和 = 回归平方和 + 残差平方和
即:(相对于样本均值)样本点的总的散布程度 = 回归线能解释的部分 + 回归线不能解释的部分
两个例子:
\[工资 = \ \ \beta_{0} + \beta_{1}学历 + u\]
\[考试成绩 = \ \ \beta_{0} + \beta_{1}复习时间 + u\]
总离差平方和的逻辑:
不同样本\(y_{i}\)是不同的
不同的人,工资不同
不同的人,考试成绩不同
\(y_{i}\)的variation,我们用\(\left( y_{i} - \overline{y} \right)^{2}\)来衡量
每个人的工资,减去样本的平均工资
每个人的成绩,减去样本的平均成绩
把上面这个差,求平方
再把所有样本的离差平方加总:SST
对\(y_{i}\)的总体分散程度的一种度量
总体上看,样本中不同人工资有多大差异
总体上看,样本中不同人成绩有多大差异
我们要做的工作,可以描述为不同人之间的”工资(成绩)的差异,能否、多大程度上,能被
学历(复习时间)“的差异所解释
= 用不同人的x的差异,来解释不同人的y的差异
我们有一条回归线:一条直线,
\[{\widehat{y}}_{i} = \beta_{0} + \beta_{1}x_{i}\]
对于每一个x,我们都有一个y的估计值,这些估计值都落在回归的直线上。
对于每一级的学历,都有一个工资的估计值
对于每小时的复习时间,都有一个考试成绩的估计值
19.18.5 拟合优度
衡量拟合优度:R方、判定系数
\[R^{2} = SSR/SST\]
在所有y的变化中,能被回归方程所解释的比例(你的模型解释了y的总体变异的百分之几)。显然\(1 - R^{2}\)就是不能被回归方程解释的部分了。
(一元)
不同人的工资有差异,不同人的学历也有差异。工资差异,能被学历差异解释的部分占多少?
不同人的考试成绩有差异,不同人的复习时间也有差异。成绩差异,能被学习时间的差异解释的部分占多少?
不同人的y有差异,不同的人的x1,x2,… 也有差异。y 的差异,能被x1,x2,…的差异所解释的部分占多少?
如果完美拟合,y完全由x1,x2,…所决定,y就会完全落在回归线上,R方=1。反之,y和x完全没有任何关系,那么R方逼近0。
调整R方:和R方原理类似,调整R方考虑到了新变量对解释总平方和的贡献,多元回归用这个较为准确。但具体公式略过。
但注意:
在社会科学的研究中,截面数据回归R方很低很正常,同时时间序列回归天然有很大的R方(即使模型是错的)
- 例如:现实社会中,影响收入的因素不计其数,我们能包括在回归中的因素终究是很有限的,这就必然导致R方不会高。这是社会科学研究的特点。
你的模型是否正确,一般并不直接取决于R方的大小。
经济学家研究经济问题,一般不是太关心R方。经济学的学术论文一般也不会讨论R方。
例:发表在《金融研究》上的一篇研究,调整R方不到0.2。

19.18.6 统计推断
t 检验
回到我们的问题。
我们从数据中估计了学历和工资的关系\({\widehat{\beta}}_{1}\),并且我们认为经验是一个重要的因素,因此作为控制变量加了进来。
\[{\widehat{工资}}_{i} = \ {\widehat{\beta}}_{0} + {\widehat{\beta}}_{1}学历_{i} + {\widehat{\beta}}_{2}经验_{i}\]
\({\widehat{\beta}}_{1}\)的解释:工作经验保持不变的情况下,平均来说,学历提高1单位,对工资变化多少的单位(学历对工资的影响)
现在又回到我们的老问题:因为样本是随机的,我们不能只看\({\widehat{\beta}}_{1}\)是大于0还是小于0:
- 可能学历和工资本质上没有关系(本质上是\(\beta_{1} = 0\)),但手里的数据偶然显示出关系(非0)
因此,对于我们研究的问题,我们还要问,\({\widehat{\beta}}_{1}\)猜测我们有多少把握?
做个相对于0的t检验!
原假设:\(\beta_{1} = 0\)(学历和工资没关系)
如果我们获得一个比较大的t值,或者很小的p值,我们就可以拒绝原假设:
如果学历和工资真的没关系,那么我们偶然估计得到的\({\widehat{\beta}}_{1}\),和0的差异如此之大,这个概率也太小了(p值很小);或者说,基本上可以认为学历和工资是有关系的,系数的解释见上。
同样:t值= 估计量 / (估计量的标准误),进而计算出p值。
上述这些值,SPSS都会帮你算好。
归根结底,你希望你所估计的统计显著的
,具有一个较大的t值,较小的p值(小于某个你选择的\(\alpha\))
F检验
t 检验:
原假设:某一个系数为0
备择假设:某一个系数不为0
F检验
原假设:全部系数都为0
备择假设:全部系数不同时为0
\[F = \frac{SSR/p}{SSE/(n - p - 1)}\]
SSR:回归平方和/解释平方和:由回归线解释的部分
SSE:残差平方和:不能由回归线解释的部分
P:解释变量的个数,一元回归时候p=1
N:样本数
P和N是SSR和SSE的自由度。
F值的直观解释:平均的SSR
对”平均的SSE”的比例
F越大:平均来说,能由回归线解释的部分SSR,比不能由回归线解释的部分SSE,就越大。
如果有一个很大的F值以及很小的P值,那么我们可以拒绝回归系数同时为0。
19.18.7 拓展:多元回归变量的选择
有2种思路,问你是希望尽可能充分地解释y,还是尽量估计某个x和y的关系?即估计一个精准的\(\beta\)?
我们会发现,SPSS不少工具是针对前者,但经济学的研究多数关心后者。
19.18.7.1 尽可能解释Y(SPSS中的工具)
如果你要尽可能的解释y,那么你需要在大量的解释变量中,选出统计显著的变量,排除不显著的变量,并获得尽量大的R方。(不得不说再次说明,经济学的研究一般不这么做)
前向筛选(Forward):将解释变量逐个添加进回归方程:
首先:把与被解释变量y相关系数最高的解释变量x放入方程,进行回归和有关的检验;
第二:在剩余的解释变量中,找到与y的偏相关系数最高的解释变量(控制已进入回归的解释变量),再放入方程,进行回归和有关的检验;
重复上述过程,把其他变量逐一加入,并逐步进行回归和有关的检验,直到再添加变量,系数不再显著,则完成。
后向筛选(Backward):将解释变量剔除回归方程:
首先:把全部解释变量放入方程,进行回归和有关的检验;
第二:在不显著的变量中,剔除t值最小的变量,进行回归和有关的检验;
重复上述过程,直到余下所有解释变量都显著。
逐步筛选(Stepwise):上述两种方法的综合。前向筛选,因为逐一添加变量,那么后添加的变量,可能使前面添加的变量不再显著(加了新的变量后,老的变量从显著变成不显著)。因此,逐步筛选会在每次添加变量时,都检查是否有变量要剔除。
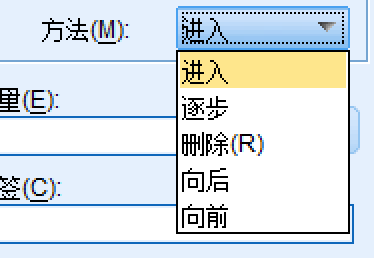
SPSS中的界面中
进入(旧翻译)/ 输入(新翻译):全部变量加入模型
逐步(旧)/ 步进(新):逐步筛选
向后(旧)/ 后退(新):后向筛选
向前(旧)/ 前进(新):前向筛选
关心因果关系(\(\beta\)及其显著性)
计量经济学关心特定的\(\mathbf{\beta}_{\mathbf{1}}\),这个变量的系数估计是否无偏,是否显著(x1是否真的影响了y,而不是你的样本给你带来的错觉。)。
\[y = \beta_{0} + \beta_{1}x_{1} + u\]
(1)
回到我们的问题,要不要把某个其他变量\(x_{2}\)加入回归?
\[y' = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + u_{1}\]
(2)
推导过程略,陈述一般性的结论:
如果x1和x2无关:那么加入一个无关变量,不影响 \({\widehat{\beta}}_{1}\)的无偏性,但会增加\({\widehat{\beta}}_{1}\)的标准误(减少t值,显著性下降,这往往不是我们希望的)
如果x1和x2有关:不放入x2,会导致x1的估计值\({\widehat{\beta}}_{1}\)有偏;放入x2,会使\({\widehat{\beta}}_{1}\)的标准误增加;
但是,在大样本的情况下,我们倾向于不管怎样,都加入x2:
因为标准误会随着样本量增大而减少(回忆t统计量)
如果加入的x2是个无关的变量,不影响 \({\widehat{\beta}}_{1}\)的无偏性,其副作用(增加\(\beta_{1}\)的标准误)会被大样本所抵消,
如果x2是个有关的变量,只有加入x2,我们关心的 \({\widehat{\beta}}_{1}\)才是无偏的,其副作用(增加\(\beta_{1}\)的标准误)也会被大样本所抵消。
结论:计量经济学看来,如果你的样本够大,那么你能想到的、可能有影响的变量都应该加进来(除了完全共线性等等约束)。
等价于:只关心我们感兴趣的变量\(\beta_{1}\)的显著性,不是很关心控制变量的显著性,统统加进来再说。(同上)
可见:很多论文,汇报回归结果时,可能有大量控制变量不显著。有些甚至直接不汇报控制变量的结果(不关心)。
例:不汇报控制变量(只告诉你控制了)只关心核心的解释变量
对比2种思路
尽量可能准确估计\(\beta\)思路:
已知要考察的变量x1,显然必须加入回归。再考虑添加控制变量,但基本不关心控制变量的显著性和R方等,只要逻辑上相关即可。
尽量充分地解释Y的思路:
追求最大化地解释y的变异(考虑R方和F值等),重点是保留显著的解释变量,因此有多种方法达成这个目标。最终可以得到一个全部解释变量都显著、R方比较大的回归。
19.18.8 共线性问题
首先,变量之间不能存在完全共线性:自变量之间不能存在完全线性关系
完全线性相关,如这个模型:
\[y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \beta_{3}x_{3} + u\]
1. 一个变量是另一个变量的两种单位的表示:x1是商品的人民币价格,x2是同商品的美元价格
2. 一个变量是另一个变量的整数倍,如x2 = 2 * x1
3. 多个变量可以组成一个线性函数,x3 = x1 + x2,或者x1+x2+x3 = 1
等等
但是:允许变量之间有相关关系,只是不能完全相关:
事物是广泛联系的,如果只让完全不相关的变量进入模型,那回归模型里面就会遗漏大量重要的信息。
解释Y的思路(非经济学的思路)
考虑一个模型
\[y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \beta_{3}x_{3} + u\]
考虑解释变量之间的相关性,直觉的办法是解释变量之间进行回归,然后看\(R^{2}\)。
1. 容忍度
\[Tol_{i} = 1 - R_{i}^{2}\]
考虑变量x1,会不会和其他变量x2,x3高度相关,把x1对另外两个解释变量进行回归
\[x_{1} = \gamma_{0} + \gamma_{1}x_{2} + \gamma_{2}x_{3} + u\]
这个回归的R方,就是\(R_{1}^{2}\),
\[Tol_{1} = 1 - R_{1}^{2}\]
显然, x1和另外2个x高度相关,\(R_{1}^{2}\)接近1,那么\(Tol_{1}\)就会接近0。
SPSS会对容忍度在0.0001之下(几乎完全线性相关)时,提出警告。
这个逻辑和计量经济学的逻辑是一致的:禁止完全线性相关(所以警告),但高度相关本身不是”错误”。
- 方差膨胀因子
\[VIF_{i} = \frac{1}{1 - R_{i}^{2}} = \frac{1}{Tol_{i}}\]
是容忍度的倒数,x1和其他解释变量的相关性越高,\(R_{1}^{2}\)就越接近1,显然VIF越大(可以大到正无穷),简单的看法是VIF是否大于10。
- 特征值和方差比
略
- 条件指数
公式略
一般而言:[0,10)之间较弱,(10,30]中度,大于30较严重
更关心\(\beta\)的思路(经济学的思路)
禁止完全共线性,所以问题就变成:如果不是完全共线性,但是变量之间还是存在相关性(称之为”多重共线性问题”),会如何?
推理过程略,只说结论:
只要不是完全共线性,变量之间相关关系,并不影响无偏性。
- 相反,你遗漏了一个相关变量(虽然相关性有点高),估计量 \({\widehat{\beta}}_{i}\)可能变成有偏的,原则上我们还是希望要一个无偏估计,最好还是加进来。
变量之间高度相关,会增加估计量 \({\widehat{\beta}}_{i}\)的方差
- 方差+,标准误+,t值下降,显著性下降,这也不是我们希望的。
多重共线性问题:不影响无偏性,但影响估计值的显著性
- 老办法:大样本降低估计量的方差,以抵消这种影响!
和你关心的变量无关:
考虑一个模型
\[y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \beta_{3}x_{3} + u\]
如果\(x_{2},x_{3}\)高度相关,那么这两个系数\(\beta_{2},\beta_{3}\)的方差可能就很大,可能使对应的t值变小,甚至不显著(比如从3掉到1)。但是,如果你感兴趣的变量是\(x_{1}\),这对你的\(\beta_{1}\)的方差和显著性没有影响!
在现实的社会科学研究中,我们都是被动的数据采集者,和实验室数据不同,采集到的数据完全无关是不可能的。我们采集不到无关的数据,但是我们可以采集到大量的数据!
总结:
- 追求无偏性:相关的控制变量应该加入。
- 抵消估计量方差的增加:大样本。
所以:在大样本下,经济学一般不太关心多重共线性问题(但禁止完全共线性)
反过来想:如果存在多重共线性,你的估计还是显著的,那么排除共线性,显然会更显著,就更加没问题了。
19.18.9 残差分析
主要几个方面:正态性(是否服从均值为0的正态分布),同方差,序列相关,和是否有异常值。
正态性
检验一个变量是否服从正态分布:K-S检验(回忆)
异方差:
随着x的不同,回归残差不再是同方差。
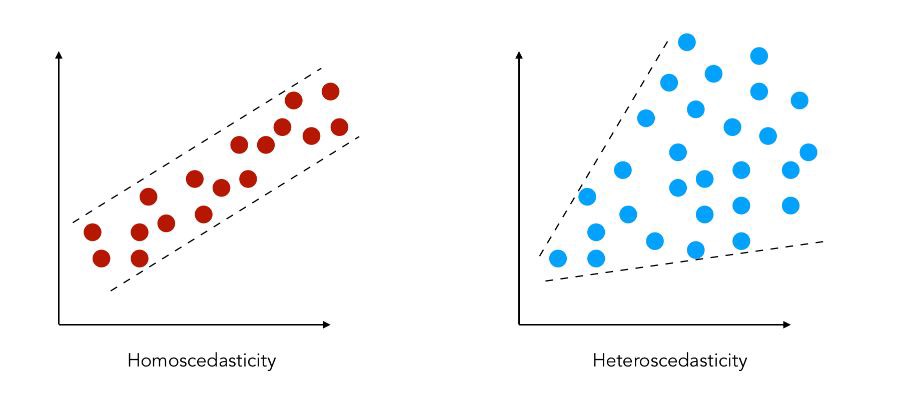
过程略,小结:
异方差不影响估计的无偏性和一致性,
异方差会让OLS计算出来的t值不服从t分布,F值不服从F分布,导致统计推断(是否显著)失效。而且这个问题,增大样本也解决不了。
可能还不知道异方差的具体形式
计量经济学的常规方案:采用异方差稳健标准误来计算t值,在计量软件(如stata)有现成的做法。如果怀疑有异方差,直接在计量软件中采用异方差稳健标准误即可。
加权最小二乘法:已知异方差的形式时可以采用的办法,但现在用得很少了,一般都是直接采用异方差稳健标准误来处理。略。
序列相关/自相关
DW检验:公式略
DW值:0,2,4划分
靠近0:正相关越强;靠近4:负相关越强;靠近2越不相关。
序列相关:可能有遗漏变量、变量存在滞后(今年的x影响明年的y:回忆货币政策时滞)等等。
具体要在时间序列分析和面板数据分析中研究,这里略。
19.18.10 虚拟变量
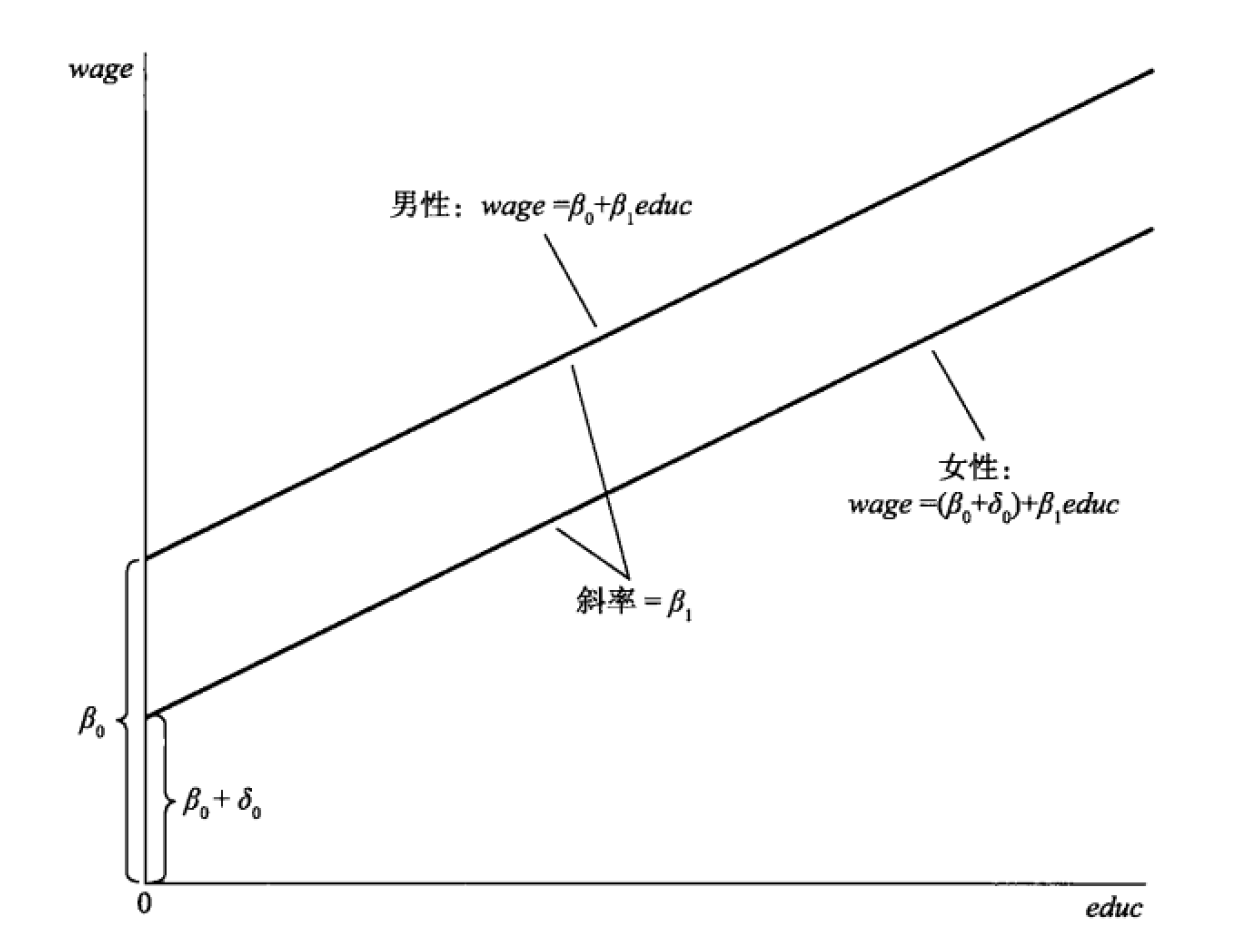
虚拟变量:分类变量,但只有01两个值(如男女、高低、及格不及格)等等。体现为回归线的截距。
如工资中加入性别:
\[工资 = \ \ \beta_{0} + \beta_{1}学历 + \beta_{2}性别 + u\]
学历的系数还是一个,即:模型中假设,不同性别的人,回归线的斜率相同
但截距不同
例如,数据中,性别=0表示男性,性别=1表示女性;代入上式
(注意,看你的数据,可能用1表示男性,后面的解释也有对应转换。)
那么男性的回归方程就是:
\[工资 = \ \ \beta_{0} + \beta_{1}学历 + u_{1}\]
女性的回归方程就是:
\[{工资 = \ \ \beta_{0} + \beta_{1}学历 + \beta_{2} + u_{1} }{= \beta_{0} + \beta_{2} + \beta_{1}学历 + u_{1}}\]
斜率相同:\(\beta_{1}\);截距不同:\(\beta_{0}\) vs \(\beta_{0} + \beta_{2}\)
考虑斜率不同
上述2个方程斜率相同:等于假定,同样的学历增加1年,男性和女性工资增幅(斜率)一样。
假如我们认为,学历的变化,对男女有不同影响呢?
估计这个模型:把性别和学历相乘
\[工资 = \ \ \beta_{0} + \beta_{1}学历 + \beta_{2}性别 + \beta_{3}(学历*性别) + u\]
那么男性的回归方程就是:
\[工资 = \ \ \beta_{0} + \beta_{1}学历 + u_{1}\]
女性的回归方程就是:
\[{工资 = \ \ \beta_{0} + \beta_{1}学历 + \beta_{2}{+ \ \beta}_{3}学历 + u_{1} }{= \beta_{0} + \beta_{2} + {(\beta}_{1}{+ \ \beta}_{3})学历 + u_{1}}\]
截距和斜率都不同了。
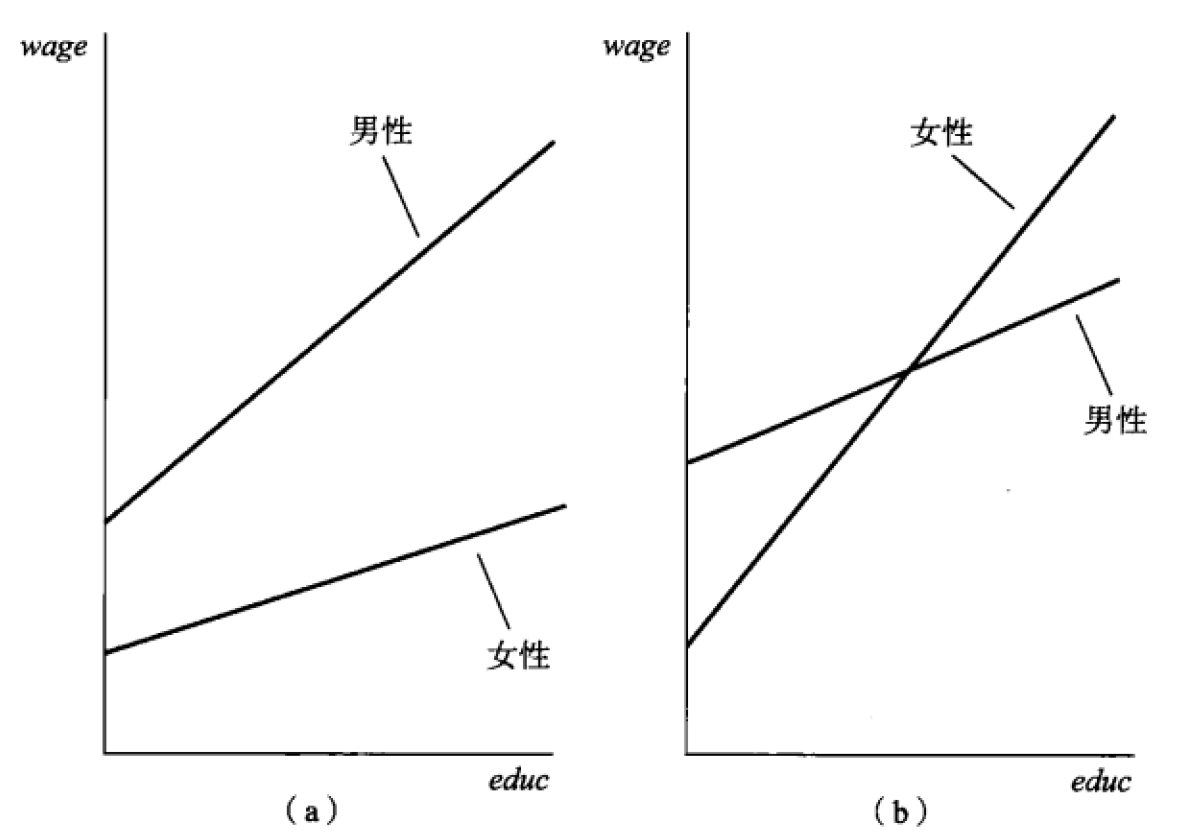
如果 \(\beta_{3}\)是显著的,那么2条先之间的斜率有显著差异:学历的变化,对男女的工资有不同影响呢。
反之,可以认为是平行的。
其他解释同前。
19.18.11 曲线估计
例如上面的模型
\[工资 = \ \ \beta_{0} + \beta_{1}学历 + u_{1}\]
显然,回归方程符合\(y = a + bx\)的形式,我们知道这是一条”直线”,所以我们也称这种模型为”线性模型”。
有很多模型,虽然直接画图,不是一条直线,如可能是抛物线(二次项)
\[y = \beta_{0} + \beta_{1}x + \beta_{2}x^{2} + u_{1}\]
但是,我们依然认为这是一个线性回归方程。
例如:随着你的工作经验的增加,你的工资会涨,但是可能不如刚入职时候涨得那么快:工作经验对于工资的提高,是边际递减。考虑到这一点,我们可以加入工作经验的二次项
\[工资 = \ \ \beta_{0} + \beta_{1}工作经验 + \beta_{2}工作经验^{2} + u_{1}\]
图形可能是这样的:开口向下的二次曲线左侧可以用来表达边际递减的性质
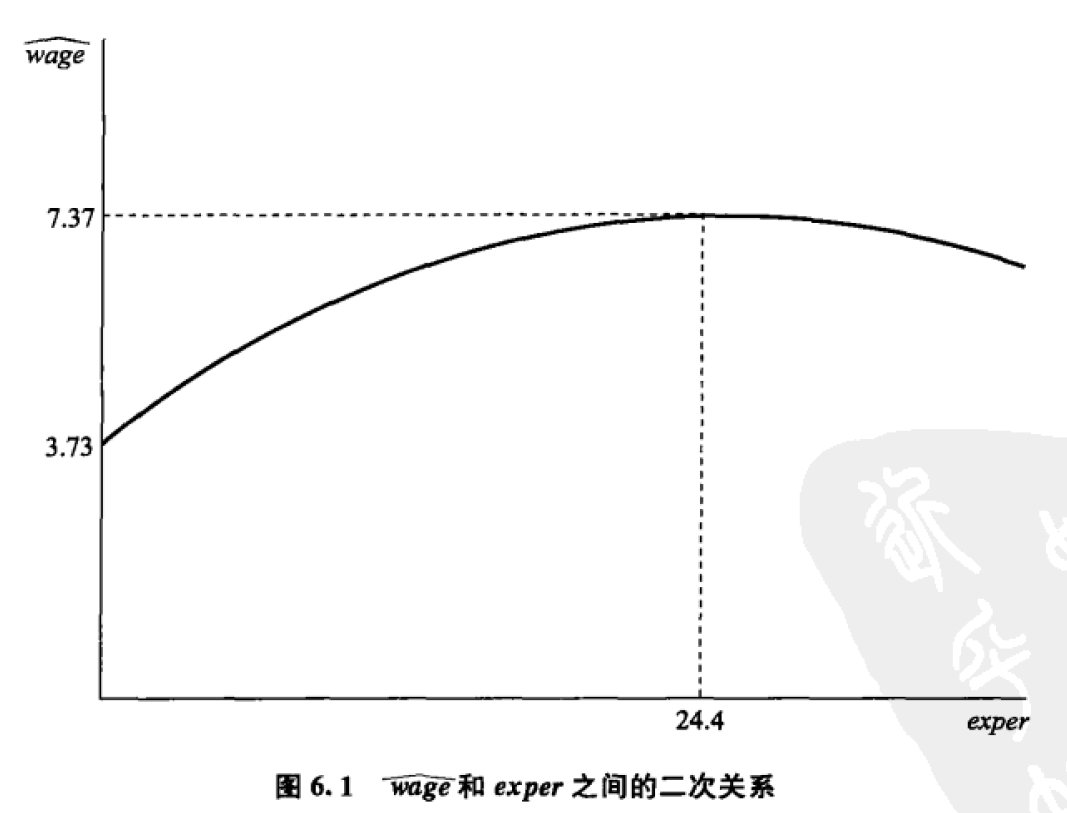
如果我们把(\(工作经验^{2}\))看成一个新的变量\(A = 工作经验^{2}\),那么上面的式子就可以变成
\[工资 = \ \ \beta_{0} + \beta_{1}工作经验 + \beta_{2}A + u_{1}\]
你会发现,这其实和原来的多元线性回归没有什么区别。
包括对数或者半对数曲线
\[y = a + b\ln x\ \]
令\(A = \ln x\)
\[y = a + bA\ \]
各种指数形曲线
\[y = e^{a + bx}\]
两边取对数:
\[\ln y = a + bx\]
令\(A = \ln y\)
\[A = a + bx\]
等等,这些x-y关系不是直线,但总是转为某种\(y = a + bx\)形式的,我们都可以采用线性估计。因为我们要估计的其实是截距a和斜率b,只要能转为上述形式曲线,都可以采用线性估计,至于x和y是怎样不论。
但是,在SPSS中,不用你手动转换,SPSS对于特定的函数类型,典型如二次型\(y = a + bx^{2}\),或者对数\(y = a + b\ln x\),SPSS都会帮你自动处理。
SPSS可以处理的函数类型(来自SPSS官网):
线性。方程为 Y = b0 + (b1 * x) 的模型。
对数。公式为 Y = b0 + (b1 * ln(x)) 的模型。
逆。方程为 Y = b0 + (b1 / x) 的模型。
二次.方程式为 Y = b0 + (b1 * x) + (b2 * x**2) 的模型。
三次.由方程 Y = b0 + (b1 * x) + (b2 * x**2) + (b3 * x**3) 定义的模型。
幂。方程式为 Y = b0 * (x**b1) 或 ln(Y) = ln(b0) + (b1 * ln(x)) 的模型。
复合。方程为 Y = b0 * (b1**x) 或 ln(Y) = ln(b0) + (ln(b1) * x) 的模型。
S 曲线。公式为 Y = e**(b0 + (b1/x)) 或 ln(Y) = b0 + (b1/x) 的模型。
Logistic。方程为 Y = 1 / (1/u + (b0 * (b1**x))) 或 ln(1/y-1/u) = ln (b0) + (ln(b1) * x) 的模型.
增长。方程式为 Y = e**(b0 + (b1 * x)) 或 ln(Y) = b0 + (b1 * x) 的模型。
指数。方程为 Y = b0 * (e**(b1 * x)) or ln(Y) = ln(b0) + (b1 * x) 的模型。
常用曲线
二次型
指数
Logistic
19.19 聚类分析
聚类分析和判别分析,都是把个案(样本、观测值)进行分类(也可以对变量进行聚类),这里先说聚类。
聚类分析:
考察样本和样本之间”距离”,把”距离”近的样本归为一类
不需要有先验知识(如类别的均值分布和其他特征等)就可以产生分类
19.19.1 分层聚类/层次聚类
基本原理
层次聚类(分层聚类)的基本原理:结合动图
先把距离最近的2个样本聚在一起,形成一个小类(p5+p6)
现存的样本中,p4和(p5+p6)距离最近,形成一个新的小类(p4+p5+p6)
现存的样本中,p1和p2的距离最近,形成一个新的小类(p1+p2)
现存的样本中,p0和(p1+p2)的距离最近,形成一个新的小类(p0+p1+p2)
现存的样本中,p3和(p4+p5+p6)的距离最近,形成一个新的小类(p3 + p4+p5+p6)
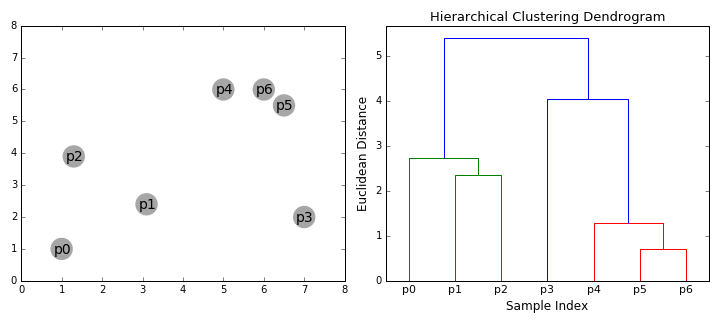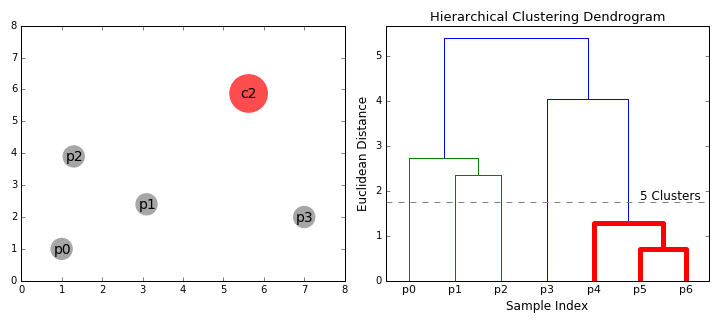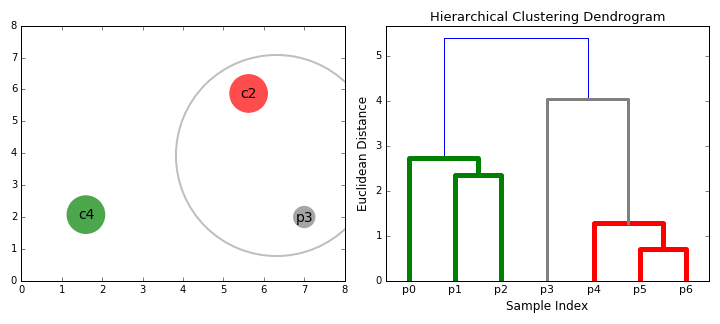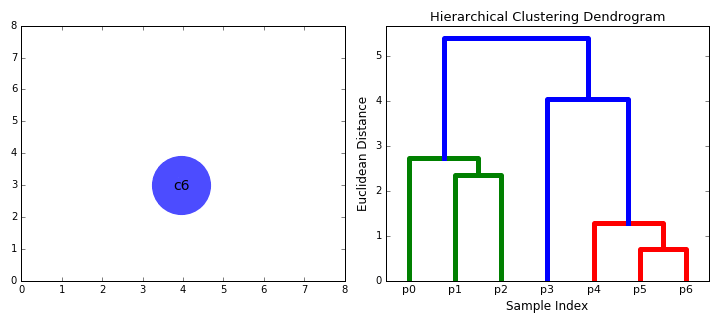
选择你需要的分类数,即可获得具体的分类。
距离
个案和个案的距离(点的距离),一般可以用:
欧氏距离:\(\rho = \sqrt{\left( x_{2} - x_{1} \right)^{2} + \left( y_{2} - y_{1} \right)^{2}}\),中学几何,最直观的”距离”
欧氏距离的平方
个案和小集合(小类)的距离:衡量一个点A,和多个点(如BCD3个点)组成的小类的距离,常用的是”组间距离”
组间平均锁链距离(between-groups linkage):
计算AB,AC,AD的距离取平均
只考虑个体与另一个组里面所有成员的距离
如果是小类和小类之间的距离,就对一个小类中所有成员,进行上述运算,再取均值。
还有组内距离:
组内平均锁链距离(within-groups linkage):
把A放进(BCD)的小类中,计算这个新的小类(ABCD),两两距离的均值
AB,AC,AD,BC,BD,CD的均值
考虑个体与另一个组里面所有成员的距离,还考虑原小类成员之间的距离
以及最近、最远、重心等。
19.19.2 K-means聚类
分层聚类:可以获得任意类别数量的分类方法,但是计算起来非常缓慢,要计算大量的两两距离。
K-means:速度快很多,但要指定类别的数量。
基本原理:
给定K个聚类数量(要分K类)
确定每个聚类的初始中心(也可以让SPSS自己求)
对于所有的点,计算到K个中心点的距离(欧氏距离),划分到最近的一个点,构成一组。
迭代:对于上述过程中划分好的K个类别,重新计算新的中心点(均值),再次进行最邻近的划分,重复这个过程N次。
一个迭代2轮的示例:
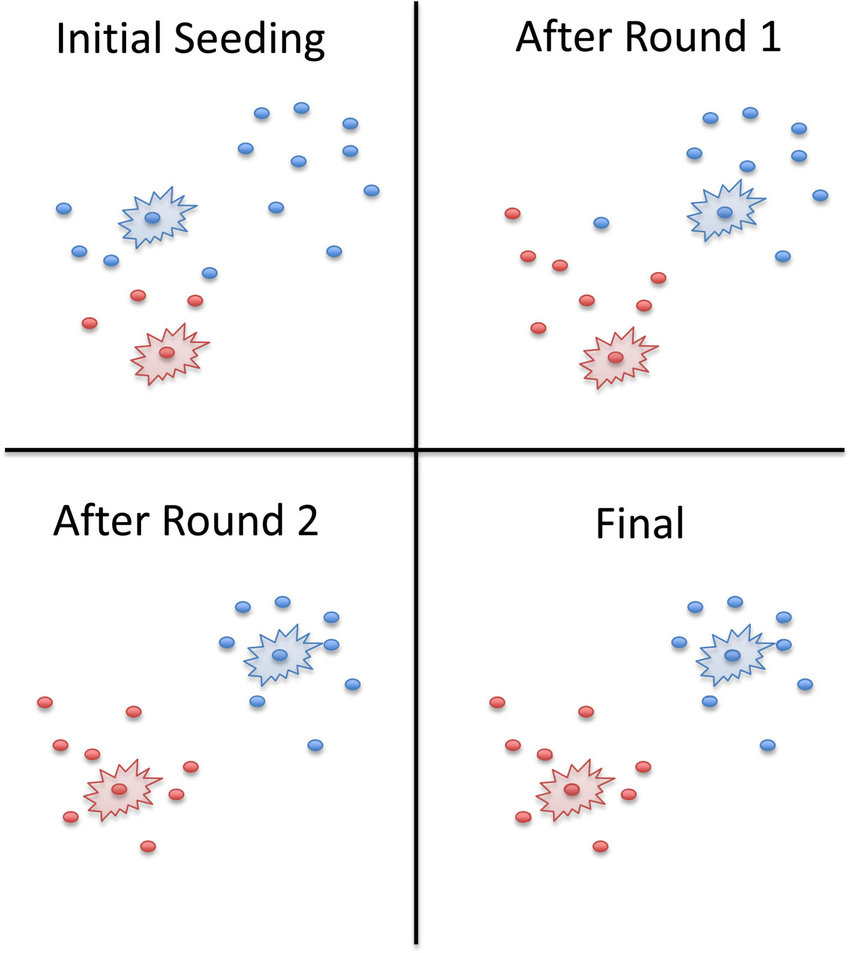
两种聚类的简单对比
K-means:
需要预先定义分类的数量
算法简单计算快,可以自定义迭代次数,利于处理大样本
如果数据分簇比较明显(不同类别的样本各自扎堆)效果较好
分层:
不用预先定义分类的数量,甚至可以在分析过程中发现分类的数量
可以发现样本之间的层次关系
计算量太大,要算非常多的两两距离,适合小样本数据
19.20 因子分析*
因子分析的目标:
大幅度减少自变量的数量
又不会丢失太多的信息
19.20.1 前提
变量之间有较高的相关性
因为变量之间有较高相关性,所以某些相关因素就可以”合并/提取共有因素”:合并
高度相关的变量,减少了自变量,又不会丢失过的信息。
一个极端的例子:如果x1和x2相关性达到0.99,那么可以认为他们几乎表示相同的信息,即使把这2个变量进行”合并”,也不会有什么损失。
例:语文,数学,外语,物理
语文和外语,用某种方式组合;数学、物理又以某种方式组合
4个变量,变成2个因子(如文科和理科)
反过来,如果变量之间毫不相关,没有重回的信息,显然就没法”合并”,自然也无法减少变量数量。
判断相关性:
相关系数矩阵:最直觉的方法。大部分相关系数<0.3,则不适合因子分析(无法合并、减少变量)
巴特利球形度检验:
原假设:相关系数矩阵为单位矩阵(对角线为1,其他为0)
直觉:如果相关系数矩阵是一个单位矩阵,那么每一个变量和其他变量的相关性都是0,即变量之间毫不相关:无法、不用做因子分析。
如果检验获得一个很小的p值:拒绝原假设,变量之间的相关性不可能全是0,可以进行因子分析。
反映像相关系数:略
KMO检验:略
因子提取和载荷计算求解
大体而言,我们把语文、数学、英语、物理成绩四个变量,缩减成2个因子(\(f_{1}\)和\(f_{2}\)),需要从数据中估计这个线性模型:
语文成绩 = \(a_{11}f_{1} + a_{12}f_{2}\)
数学成绩 = \(a_{21}f_{1} + a_{22}f_{2}\)
英语成绩 = \(a_{31}f_{1} + a_{32}f_{2}\)
物理成绩 = \(a_{41}f_{1} + a_{42}f_{2}\)
算法略,SPSS中也是自动完成的。
最终可以把\(a_{ij}\)算出,并计算出2个新的变量\(f_{1},\ f_{2}\),这2个变量可以保留以前4个变量(语数英外)的大部分信息。
19.21 判别分析 *
根据现有的数据,计算出分类模型,并以此对新的数据进行归类。
如:现有数据包括了健康人和病人(2个类别)的各种体征(体温、血压等),从一份新的体征数据(体温、血压等),判断这个人属于健康人还是病人(新数据应该归入哪类)
聚类分析 vs 判别分析
都是分类,但:
聚类分析:
并不需要知道现有样本的类别,
只要样本可以算出”距离”,就可以按距离的远近进行分类(把距离近的归为一类)
要处理新数据,就要把新数据放入原来的数据中,从头开始聚类。
判别分析:
需要知道现有样本的类别,从现有的分类数据中获得一个分类模型
可以按这个模型,对新数据进行判断。
判别分析比较像回归分析
回归:用自变量来解释一个(一般是)连续的因变量:复习时间解释考试成绩
判别:用自变量解释一个离散的因变量:按叶片的尺寸,对鸢尾花的品种进行分类。
详细的原理略。