Code
# 以下都是例行公事,直接拷贝即可
import pandas as pd
import numpy as np
# 导入matplotlib.pyplot绘图库,其中plt.plot()是最常用的绘图函数之一
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme() # 默认用seaborn的绘图样式
# 设置字体。如果不设置,中文可能会乱码。这里采用冬青黑、微软雅黑和文泉驿微米黑,可以兼容大多数操作系统。
plt.rcParams["font.sans-serif"]=["Hiragino Sans GB", "Microsoft YaHei", "WenQuanYi Micro Hei"]
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题
# 绘图使用'svg'后端:svg是矢量格式,可以任意缩放均保持清晰,各种屏幕的显示良好。
%config InlineBackend.figure_formats = ['svg']
快速复习
这里快速复习一下Markowitz资产组合模型,详情可见大部分投资学教材(如博迪的《投资学》)的相关章节。
2种资产的组合
考虑2种资产的组合,期望收益分别是\(r_1,r_2\),各自的方差分别是\(\sigma_1^2, \sigma_2^2\)。投资的权重是\(w_1, w_2\),其中\(w_1+ w_2 = 1\)。
那么组合期望收益就是:(简便起见这里就不写成期望形式了)
\[
r_p = w_1 r_1 + w_2 r_2
\]
组合的方差就是:
\[
\sigma_p^2 = w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + 2 w_1 w _2 \operatorname{Cov}(r_1,r_2)
\]
一个随机变量的方差,就是它自己和自己的协方差,因此上式又可以写成:
\[
\sigma_p^2 = w_1^2 \operatorname{Cov}(r_1,r_1)+ w_2^2 \operatorname{Cov}(r_2,r_2) + 2 w_1 w _2 \operatorname{Cov}(r_1,r_2)
\]
上面的式子可以用协方差矩阵的形式来表示:
| \(w_1\) |
\(\operatorname{Cov}(r_1,r_1)\) |
\(\operatorname{Cov}(r_1,r_2)\) |
| \(w_2\) |
\(\operatorname{Cov}(r_2,r_1)\) |
\(\operatorname{Cov}(r_2,r_2)\) |
可见,组合的方差,就等于上面的矩阵中的每一个协方差,乘以对应的权重,再相加。
直接从上式可以得到结论:
- 如果2种资产是负相关,那么他们的协方差就是负数(看最后一项),组合的方差必然下降。
- 如果2种资产是正相关,但相关系数小于1,组合的标准差依然会低于2项资产的标准差的加权平均。
注意到,收益和方差计算中,唯一的变量是权重,那么我们可以把每一个权重,对应的收益和标准差计算出来,绘制在一张图上。
- 选择第1个权重,如(0,1),计算代入2个公式,计算\(r_{p1},\sigma_{p1}\)
- 选择第2个权重,如(0.1,0.9),计算代入2个公式,计算\(r_{p2},\sigma_{p2}\)
- 选择第3个权重,如(0.2,0.8),计算代入2个公式,计算\(r_{p3},\sigma_{p3}\)
- …
把上述收益和标准差的组合绘制出来,你会得到下图中一组曲线的其中一条,称为“投资组合可行集”。
横轴是标准差,纵轴是收益。(图来自博迪《投资学》11版)
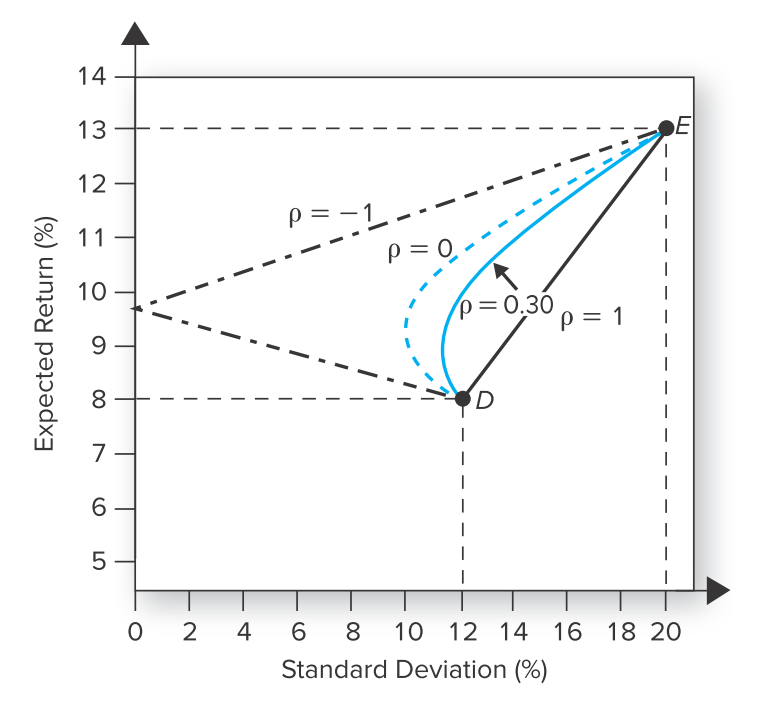
如果2种资产的相关性:
- 等于1,则组合的标准差是2者标准差的线性组合。
- 小于1,则组合会有一个最小方差点(最小标准差点):在这个组合下你可以获得最小方差。(两天蓝色线)
- 等于-1,则某个组合可以让最小方差为0。
资产配置
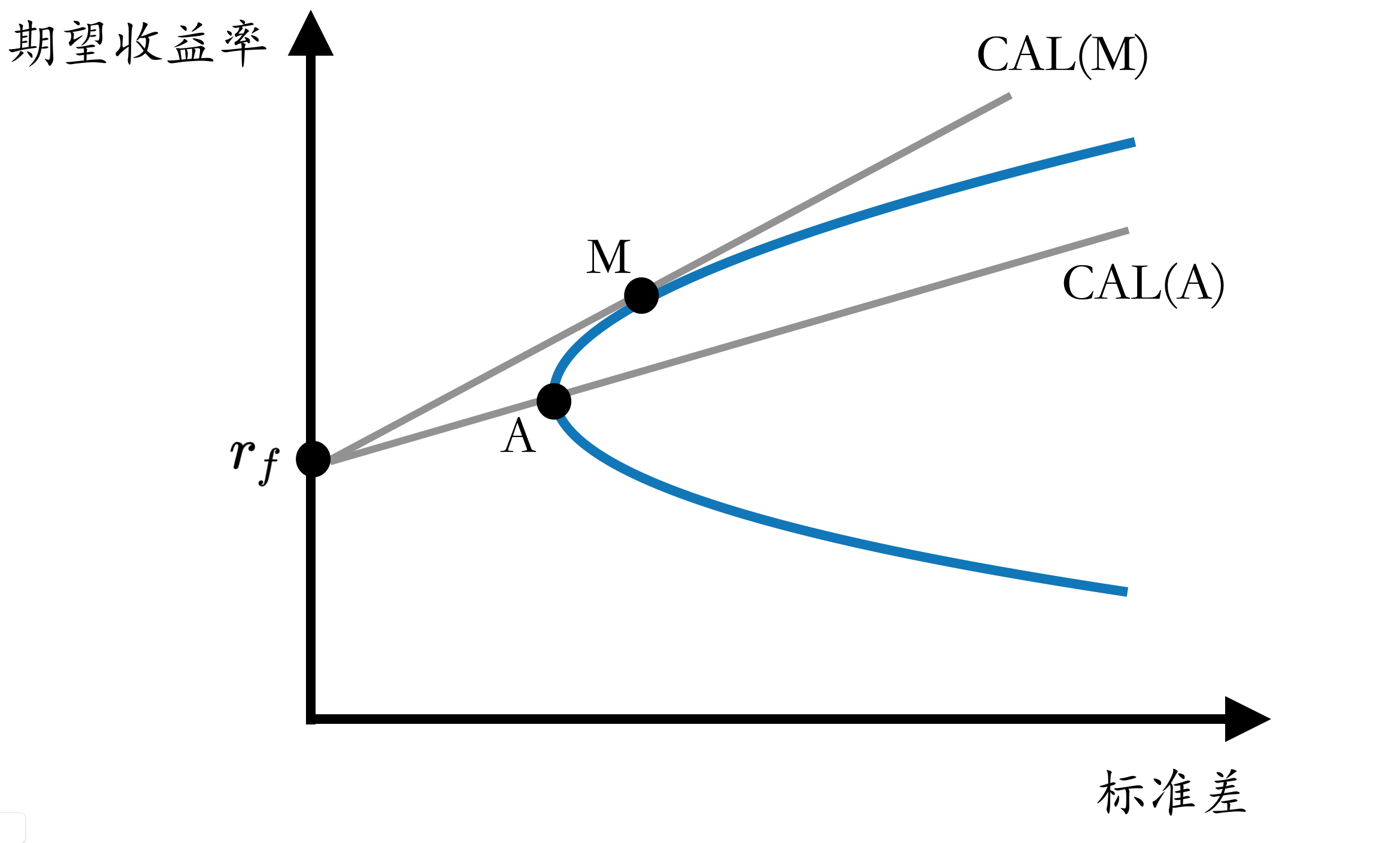
引入无风险资产,比如国债等等。考虑无风险资产和风险资产的组合。因为无风险资产和组合之间的协方差为0,那么无风险资产和风险资产的组合的期望收益和方差的关系,就是一条直线。
称为:“资本配置线(CAL)”:
- 如果全部投资于无风险资产,那么你获得了无风险收益率,同时组合方差为0:射线的最左端。
- 随着你增加风险资产的比例,那么方差也等比增加:因此是一条射线。
- 风险资产组合有无限种(权重的不同),反映为蓝色曲线(投资组合可行集)上的每一个点。那么纳入无风险资产,就是从\(r_f\)点,引出一条射线,穿过蓝线上的某个点。
- 射线斜率就是夏普比率:衡量每单位风险,能够获得多少超额收益。
- 所以穿过哪个点是最优的?斜率最高那条,即切线,则切点为“最优风险组合”。
\[
S_p=\frac{\mathrm{E}\left(r_p\right)-r_f}{\sigma_p}
\]
马科维茨资产组合选择模型
把2种资产的情况扩展到n种,那么上面的2资产公式可以推为:
组合的期望收益:
\[
r_p = \sum_{i=1}^n {w_i r_i}
\]
组合的方差:
\[
\sigma_p^2 = \sum_{j=1}^n \sum_{i=1}^n w_i w_j \operatorname{Cov}(r_i,r_j)
\]
可以想象把前面的矩阵扩展到n行n列。
令\(w\)为权重,\(\Sigma\)为协方差矩阵,上面的式子可以写成矩阵:
\[
\sigma_p^2 = w^t \Sigma w
\]
(w的转置,乘以协方差矩阵,乘以w)
我们要做的,就是用蒙特卡洛模拟的方法(近似可以理解为穷举法),尝试极大量的组合,计算他们的收益和标准差,绘制在图上,最后计算出最佳的组合权重。
蛮力计算正是电脑擅长的。
数据来源
但后面的讲义示范会使用预先制作的范例数据(包括3只股票)。这里先简单介绍怎么获得股票的价格数据,最简单的方法,是用akshare这个包。akshare这个包可以提供大量的金融数据,说明在这个地址 https://akshare.akfamily.xyz/introduction.html
- 简单安装:在任何一个python单元格,执行以下代码,会从清华大学的镜像服务器下载并安装(注意开头有个感叹号):
!pip install -i https://mirrors.tuna.tsinghua.edu.cn/pypi/web/simple akshare
当然,安装只要执行一次即可,今后使用不必再次安装。
查看说明文档 https://akshare.akfamily.xyz/introduction.html
我们需要用A股的历史行情数据,说明在这里 https://akshare.akfamily.xyz/data/stock/stock.html#id21
使用东方财富网作为数据源,说明在这里‘https://akshare.akfamily.xyz/data/stock/stock.html#id22’
例如,我们要读取平安银行(000001)的历史行情,可以这么写,这里采用”前复权”
注意:和akshare自己的说明不同,当前复权时候,日收益率才是正确的。如果你装了炒股软件,可以打开来看。
import akshare as ak
df = ak.stock_zh_a_hist(symbol="000001", period="daily", start_date="20170301", end_date='20241231', adjust="qfq")
df.iloc[:10,:10] # 查看前10行,和前10列
| 0 |
2017-03-01 |
000001 |
7.18 |
7.18 |
7.24 |
7.16 |
346994 |
330157968.0 |
1.12 |
0.14 |
| 1 |
2017-03-02 |
000001 |
7.20 |
7.12 |
7.23 |
7.11 |
403629 |
382395888.0 |
1.67 |
-0.84 |
| 2 |
2017-03-03 |
000001 |
7.10 |
7.09 |
7.12 |
7.05 |
342655 |
321952544.0 |
0.98 |
-0.42 |
| 3 |
2017-03-06 |
000001 |
7.09 |
7.14 |
7.15 |
7.08 |
404511 |
381212304.0 |
0.99 |
0.71 |
| 4 |
2017-03-07 |
000001 |
7.13 |
7.14 |
7.15 |
7.09 |
294673 |
277747408.0 |
0.84 |
0.00 |
| 5 |
2017-03-08 |
000001 |
7.12 |
7.11 |
7.14 |
7.09 |
244438 |
230425150.0 |
0.70 |
-0.42 |
| 6 |
2017-03-09 |
000001 |
7.10 |
7.07 |
7.12 |
7.05 |
378170 |
354813680.0 |
0.98 |
-0.56 |
| 7 |
2017-03-10 |
000001 |
7.07 |
7.09 |
7.10 |
7.05 |
390182 |
366140048.0 |
0.71 |
0.28 |
| 8 |
2017-03-13 |
000001 |
7.08 |
7.13 |
7.14 |
7.06 |
545304 |
513148480.0 |
1.13 |
0.56 |
| 9 |
2017-03-14 |
000001 |
7.12 |
7.13 |
7.15 |
7.10 |
404484 |
381594064.0 |
0.70 |
0.00 |
Index(['日期', '股票代码', '开盘', '收盘', '最高', '最低', '成交量', '成交额', '振幅', '涨跌幅', '涨跌额',
'换手率'],
dtype='object')
在后续的例子中,我们使用收益率序列(后面会讲为什么),因此暂时只需要日期和涨跌幅两列。
sh000001_df = df[['日期','涨跌幅']].copy()
sh000001_df.columns = ['日期', '平安银行']
sh000001_df
| 0 |
2017-03-01 |
0.14 |
| 1 |
2017-03-02 |
-0.84 |
| 2 |
2017-03-03 |
-0.42 |
| 3 |
2017-03-06 |
0.71 |
| 4 |
2017-03-07 |
0.00 |
| ... |
... |
... |
| 1890 |
2024-12-09 |
0.09 |
| 1891 |
2024-12-10 |
1.03 |
| 1892 |
2024-12-11 |
-0.51 |
| 1893 |
2024-12-12 |
1.02 |
| 1894 |
2024-12-13 |
-2.45 |
1895 rows × 2 columns
同理,你可以下载任何你想要分析的股票的数据。
假如你要做n只股票的最优组合,你只要下载n只股票的数据,然后merge起来即可。
组合的预期收益和方差
范例数据returns.xlsx,里面包含了3只股票的日回报率数据。
# 读取数据并查看
df = pd.read_excel('data/returns.xlsx',converters={'日期':pd.to_datetime})
df.set_index('日期',inplace=True)
df.head()
| 日期 |
|
|
|
| 2019-01-02 |
-0.035882 |
-0.011394 |
-0.020256 |
| 2019-01-03 |
-0.022575 |
-0.006586 |
0.009793 |
| 2019-01-04 |
0.053891 |
0.021823 |
0.050647 |
| 2019-01-07 |
0.014610 |
0.000000 |
-0.001026 |
| 2019-01-08 |
0.028994 |
-0.003514 |
-0.008214 |
收益率等于 \[
r_1 = x_1/x_0 - 1
\]
对数收益率等于 \[
lr_1 = \ln {x_1/x_0} = \ln(r_1 + 1)
\]
从对数收益率算收益率 \[
r_1 = e^{lr_1} - 1
\]
为什么要用对数收益率?因为对数收益率具有可加性:持有2个时间段的收益率的对数,正好是2个时间段,各自对数收益率的直接相加。
\[
lr_{12} = lr_1 + lr_2
\]
如果不取对数,算起来会更麻烦:
\[
1 + r_{12} = (1 + r_1) * (1+r_2)
\]
取对数后,求和、求均值等等,都更加简单了:
- 要算一段时间的收益率,只要从第一个交易的对数收益率,一直累加,加到最后一个交易日的对数收益率,就是这段时间的对数收益率。
- 要算年化收益率,求整个序列的日平对数收益率,再乘以一年的交易日250即可。
从收益率计算对数收益率
rets = np.log(df + 1)
rets.head()
| 日期 |
|
|
|
| 2019-01-02 |
-0.036542 |
-0.011459 |
-0.020464 |
| 2019-01-03 |
-0.022834 |
-0.006608 |
0.009745 |
| 2019-01-04 |
0.052489 |
0.021588 |
0.049406 |
| 2019-01-07 |
0.014504 |
0.000000 |
-0.001027 |
| 2019-01-08 |
0.028582 |
-0.003520 |
-0.008248 |
利用收益率,我们可以算出期初投资1元的净值走势,(收益率+1)累乘即可,注意这里用普通收益率(非对数)
# 计算年化收益率
rets.mean()*250 # 对数收益率的可加性,求“均值 * 一年的交易日数”,就是年化(对数)收益率
比亚迪 0.688826
美的集团 0.531378
平安银行 0.385595
dtype: float64
rets.cov() * 250 # 年化协方差矩阵
| 比亚迪 |
0.226201 |
0.054389 |
0.046846 |
| 美的集团 |
0.054389 |
0.098938 |
0.051926 |
| 平安银行 |
0.046846 |
0.051926 |
0.108442 |
给定权重的情况
要求最优组合,首先:
- 给定权重,计算出这个组合年化收益率和方差。
- 随机生成大量权重,计算计算这些随机权重的组合年化收益率和方差。
- 绘制在图上。
第一步,我们首先求随便任何一个组合的情况。
首先,随机生成3个权重:
# 证券数量 number of assets
noa = rets.shape[1]
noa
weights = np.random.random(noa) # 生成3个随机数
weights /= np.sum(weights) # 使3个随机数的和为1
weights # 三只股票的占比(这里是随机的)
array([0.27686346, 0.28901009, 0.43412646])
计算组合的方差
\[
\sigma_p^2 = w^t \Sigma w
\]
np.dot(weights.T, np.dot(rets.cov() * 250 , weights)) # 矩阵乘法满足结合律
显然标准差就是方差开根号
np.sqrt(np.dot(weights.T, np.dot(rets.cov() * 250, weights)))
写2个函数,计算在特定的权重下,股票的收益率和方差。
rets:对数回报率的序列 rets.mean():日均对数收益率 rets.mean() * weights :乘以权重后的日均对数收益率
比亚迪 0.000763
美的集团 0.000614
平安银行 0.000670
dtype: float64
def port_ret(weights):
"""年化对数收益率
"""
return np.sum(rets.mean() * weights) * 250
def port_vol(weights):
"""年化收益率的标准差
"""
return np.sqrt(np.dot(weights.T, np.dot(rets.cov() * 250 , weights)))
下一步,既然我们可以计算一组权重的情况,我们循环N次,每次随机生成一组权重,然后计算年化收益率和年化标准差。我们就可以获得N组(收益率, 标准差,权重)的组合。
prets = [] # 收益率
pvols = [] # 标准差
w = [] # 权重
for p in range (5000): # 重复5000次
# 生成一个随机权重
weights = np.random.random(noa)
weights /= np.sum(weights) # 每次重复,都随机取得3个权重。
w.append(weights)
# 计算
prets.append(port_ret(weights)) # 计算组合收益
pvols.append(port_vol(weights)) # 计算组合标准差
prets = np.array(prets)
pvols= np.array(pvols)
最小方差点
# pvols保存了所有标准差
# np.where(pvols == min(pvols): 标准差最小的那个权重是几号?
i = (np.where(pvols == min(pvols)))[0][0]
w[i].round(3) # 权重
array([0.134, 0.464, 0.402])
绘图
把前面随机生成的5000个权重,以及对应的收益和标准差,绘制在图上。
横轴是标准差,纵轴是收益率。
在最小方差点上画一个x。
plt.figure(figsize=(8, 5))
plt.scatter(pvols, prets, c=prets / pvols,
marker='o', cmap='coolwarm',s = 5,alpha=0.5)
plt.colorbar(label='Sharpe ratio(rf=0)'); #
plt.scatter(pvols[i],prets[i],c='k',s = 50,marker='x') # 最小方差点
plt.xlabel('SD')
plt.ylabel('预期收益率') ;
练习1
请你自选几只股票或者合约(不少于3只)
- 下载并整合数据
- 完成上述蒙特卡洛模拟过程
- 计算最小方差点并绘图
风险资产的有效边界
前面我们绘制了预期收益和标准差之间从关系,显然给定收益,正常人都会选择风险最小的组合,即风险资产的最小方差边界,就是上图中全部点所在区域的左侧边界。
在最小方差边界中,最小方差点之上的部分,称为风险资产有效边界。在这条线上点,表示给定收益的最小风险,或者给定风险的最大收益。
显然,我们实际会选择的组合必然在条线上。
最小标准差组合
我们的做法是给定一个收益率,比如0.55,然后求标准差最低的组合:散点图中,y=0.55横线上最右侧的点。注意,每一个点都是一个组合或者说一个权重(3只股票的比例)。
显然,这是一个约束求极值问题:
- 求使得标准差最小化的权重(类比:使得效用最大化的消费束)
- 约束1:权重之和 = 1
- 约束2:由权重算出来的收益率 = 给定的收益率0.55(实际上把整个问题约束在y=0.55这条横线上)
注意:这是的自变量是权重。
具体的过程见数学工具章节。
import scipy.optimize as sco
tret = 0.55 # 目标收益率
# 1. 区间
bnds = tuple((0, 1) for x in weights) # 3个权重的区间都是0到1
bnds
# 2. 两个紧约束(相等关系):
# 这里 x = (w1,w2,w3)
cons = ({'type': 'eq', 'fun': lambda x: port_ret(x) - tret}, # 通过 x = (w1,w2,w3) 算出来的收益率,应该等于我们指定的收益率
{'type': 'eq', 'fun': lambda x: np.sum(x) - 1}) # 权重之和 = 1
# 3. 猜测一个权重,这里就用均值 (1/3,1/3,1/3)
eweights = np.array(noa * [1. / noa, ])
eweights
array([0.33333333, 0.33333333, 0.33333333])
# 4. 最小化
# 参数:1. 最小化的目标函数:标准差函数
# 2. 你猜测(等权1/3)
# 3. 最优化算法(不展开)
# 4. 取值范围
# 5. 2一个约束
res = sco.minimize(port_vol, eweights, method='SLSQP',
bounds=bnds, constraints=cons)
给定tret = 0.55,最小的标准差是
对应的权重是
array([0.27144962, 0.56311773, 0.16543265])
综合来说:当我们把3只股票按上述比例配置,那么在这段历史数据中,我们可以获得0.55的对数收益率,且达到最小标准差 0.29。
下一步,把这个过程写成函数:参数是目标收益率,计算出最小的标准差。
def find_min_sd(tret):
'''对于指定的收益率tret,找到最小标准差的组合,并返回标准差'''
bnds = tuple((0, 1) for x in weights) # 3个权重的区间都是0到1
cons = ({'type': 'eq', 'fun': lambda x: port_ret(x) - tret},
{'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
eweights = np.array(noa * [1. / noa, ])
res = sco.minimize(port_vol, eweights, method='SLSQP',
bounds=bnds, constraints=cons)
return res.fun
find_min_sd(0.55)
计算有效边界
对于0.45到0.68之间的收益率,切成50份,对其中每一个收益率,都计算小标准差组合。
trets = np.linspace(0.45, 0.68, 50) # 切成50份
tvols = np.array([find_min_sd(tret) for tret in trets]) # 对这50个目标收益率,我们都计算最小标准差组合
问,最小方差点是第几个?
i = np.where(tvols == min(tvols))[0][0] # 最
这50个点就是有效边界:表达了收益率(y),和达到收益的最小标准差(x)的关系。因此我可以绘制在图上,并连成1条线。
注意到:我们只需要在最小方差点之上(i之后)的点。
plt.figure(figsize=(8, 5))
# 绘制散点图
plt.scatter(pvols, prets, c=prets / pvols,
marker='o', cmap='coolwarm',s = 5,alpha=0.5)
plt.colorbar(label='Sharpe ratio(rf=0)');
# 绘制有效边界
plt.plot(tvols[i:],trets[i:],c='blue',lw=3)
#plt.scatter(tvols[i], trets[i], c='k',s = 50,marker='x')
plt.xlabel('SD')
plt.ylabel('预期收益率') ;
练习2
在练习1的基础上,计算并绘制你的组合的有效边界
资本市场线
把无风险资产加入组合
令资本市场线 为 \(y = a + b x\),有效边界为\(y=f(x)\),有几个条件:
- 截距=无风险利率
- 资本市场线和有效边界在\(x\)处相交
- 资本市场线和有效边界在\(x\)处斜率相等
令有有效边界为\(f(x)\),资本市场线会与有效边界相切,那么在切点\(x\)上,两者的一阶导数相等。
\[
b = f'(x)
\]
显然,我们要解这个方程,求得切点。解方程的方法,见前面的数学工具。
有效边界是我们用模拟方法(大量的取点)计算出来的,有效边界的数据本质上以一系列的点,如何获得有效边界的一阶导数?
splrep()函数:可以对给定的x序列和y序列,拟合一条样条曲线。splev()函数:利用上一步获得的曲线,可以对x求函数值或者一阶导函数的值。
import scipy.interpolate as sci
ind = np.argmin(tvols)
evols = tvols[ind:] # 有效边界的横轴(标准差)
erets = trets[ind:] # 有效边界的纵轴(收益率)
# 获得有效边界的样条曲线
tck = sci.splrep(evols, erets)
def f(x):
''' 有效边界函数 (样条曲线逼近). '''
return sci.splev(x, tck, der=0)
def df(x):
''' 样条曲线函数的一阶导函数 '''
return sci.splev(x, tck, der=1)
对于任何一个\(x\),我们都可以获得有效边界的值\(f(x)\),以及一阶导数\(f'(x)\)
x = 0.325
print(f'{f(x)=}, {df(x)=}')
f(x)=array(0.60642485), df(x)=array(0.87363673)
我们令 \(p = \{a,b,x\}\),分别表示资本市场线的截距、斜率、以及切点的横坐标。
令资本市场线为\(y = a + bx\),我们的目标是求出参数a和b。
资本市场线的三个条件,可以写成方程组:
- 截距=无风险利率, \(a = r_f\) :
a = rf
- 资本市场线和有效边界在\(x\)处相交,\(f(x) = a + b*x\):
f(x) = a + b * x
- 资本市场线和有效边界在\(x\)处斜率相等,\(b = f'(x)\):
b = df(x)
用fsolve()函数可以解这个方程,参数分别是:
- 方程组。
- 初始参数:这是你对解的合理的猜测。如果猜得太远,就无法给出正确的解。
我们猜测,无风险利率给定为0.05,斜率猜测是1左右(45°),切点大概在0.3附近,那么我们对p的猜测就是[0.05, 1, 0.3]。
# 资本市场线的方程组
def equations(p, rf=0.05):
a,b,x = p
eq1 = rf - a
eq2 = a + b * x - f(x)
eq3 = b - df(x)
return eq1, eq2, eq3
# 求解方程组
opt = sco.fsolve(equations, [0.05, 1, 0.3])
看看求解的结果:
opt # 分别是rf = a, b, x 。其中x是切点所在的SD。
array([0.05 , 1.75627377, 0.29341009])
把求解的结果代入方程组,看看是不是所有方程都为0。
np.round(equations(opt), 4)
绘图
plt.figure(figsize=(10, 6))
# 散点
plt.scatter(pvols, prets, c=(prets - 0.05) / pvols,
marker='.', cmap='coolwarm')
# 有效边界
plt.plot(evols, erets, 'b', lw=4.0)
# 资本市场线
cx = np.linspace(0.0, 0.4)
plt.plot(cx, opt[0] + opt[1] * cx, 'r', lw=1.5)
# 切点
plt.plot(opt[2], f(opt[2]), 'y*', markersize=15.0)
plt.xlabel('SD')
plt.ylabel('预期收益率')
plt.colorbar(label='Sharpe ratio')
plt.xlim((0.25,0.5)) # 绘图的范围,可以自行调整
plt.ylim((0.35,0.7));
求切点组合
注意到,opt[2]就是切点的横坐标(SD),那么f(opt[2])就是切点的纵坐标(预期收益率)
按照我们前面求有效边界上一个点的方法:指定预期收益率,求最小化波动率的组合,代码基本一样。
cons = ({'type': 'eq', 'fun': lambda x: port_ret(x) - f(opt[2])}, # 指定的预期收益率
{'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
res = sco.minimize(port_vol, eweights, method='SLSQP',
bounds=bnds, constraints=cons)
res['x'].round(2)
array([0.31, 0.59, 0.1 ])
因此,切点组合就是:31%的比亚迪,59%的美的集团,10%的平安银行。进一步,你可以在无风险资产(\(r_f = 0.05\))和切点组合之间进行选择你希望的比例,构成最终组合。
练习3
在练习1和练习2的基础上,计算你的最优组合,绘图,并算出切点组合中每只股票的权重。

